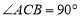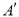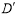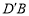题目内容
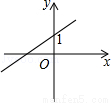
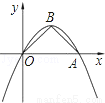
如图,抛物线y=ax2+bx经过点A(4,0),B(2,2).连接OB,AB.
(1)求该抛物线的解析式;
(2)求证:△OAB是等腰直角三角形;
(3)将△OAB绕点O按顺时针方向旋转135°得到△OA′B′,写出△OA′B′的边A′B′的中点P的坐标.试判断点P是否在此抛物线上,并说明理由.
(1)y=-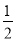 x2+2x;(2)证明见解析;(3)(-
x2+2x;(2)证明见解析;(3)(-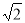 ,-2
,-2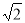 );点P不在二次函数的图象上.
);点P不在二次函数的图象上.
【解析】
试题分析:(1)将A、B的坐标代入抛物线的解析式中,通过联立方程组即可求出抛物线的解析式;
(2)过B作BC⊥x轴于C,根据A、B的坐标易求得OC=BC=AC=2,由此可证得∠BOC、∠BAC、∠OBC、∠ABC都是45°,即可证得△OAB是等腰直角三角形;
(3)当△OAB绕点O按顺时针方向旋转135°时,OB′正好落在y轴上,易求得OB、AB的长,即可得到OB′、A′B′的长,从而可得到A′、B′的坐标,进而可得到A′B′的中点P点的坐标,然后代入抛物线中进行验证即可.
试题解析:(1)由题意得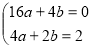 ,
,
解得 ;
;
∴该抛物线的解析式为:y=-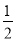 x2+2x;
x2+2x;
(2)过点B作BC⊥x轴于点C,则OC=BC=AC=2;
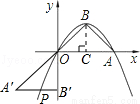
∴∠BOC=∠OBC=∠BAC=∠ABC=45°;
∴∠OBA=90°,OB=AB;
∴△OAB是等腰直角三角形;
(3)∵△OAB是等腰直角三角形,OA=4,
∴OB=AB=2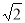 ;
;
由题意得:点A′坐标为(-2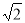 ,-2
,-2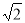 )
)
∴A′B′的中点P的坐标为(-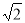 ,-2
,-2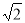 );
);
当x=-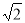 时,y=-
时,y=-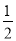 ×(-
×(-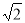 )2+2×(-
)2+2×(-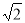 )≠-2
)≠-2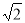 ;
;
∴点P不在二次函数的图象上.
考点:二次函数综合题.

练习册系列答案
相关题目