题目内容
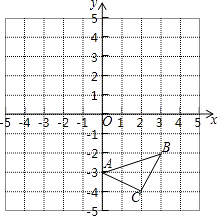
【题目】如图,在每个小正方形的边长为1的网格中,A,E为格点,B,F为小正方形边的中点,C为AE,BF的延长线的交点.
(1)AE的长等于;
(2)若点P在线段AC上,点Q在线段BC上,且满足AP=PQ=QB,请在如图所示的网格中,用无刻度的直尺,画出线段PQ,并简要说明点P,Q的位置是如何找到的(不要求证明) .
【答案】
(1)![]()
(2)AC与网格线相交,得到P,取格点M,连接AM,并延长与BC交予Q,连接PQ,则线段PQ即为所求
【解析】解:(1)AE= ![]() =
= ![]() ;
;
故答案为: ![]() ;
;
(2)如图,AC与网格线相交,得到P,取格点M,连接AM,并延长与BC交予Q,连接PQ,则线段PQ即为所求.
故答案为:AC与网格线相交,得到P,取格点M,连接AM,并延长与BC交予Q,连接PQ,则线段PQ即为所求.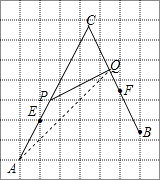
(1)根据勾股定理即可得到结论;(2)取格点M,连接AM,并延长与BC交予Q,连接PQ,则线段PQ即为所求.本题考查了作图﹣应用与设计作图,勾股定理,正确的作出图形是解题的关键.

练习册系列答案
相关题目