Question

【题目】小明上学途中要经过A，B两地，由于A，B两地之间有一片草坪，所以需要走路线AC，CB，如图，在△ABC中，AB=63m，∠A=45°，∠B=37°，求AC，CB的长．（结果保留小数点后一位）
参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75， 取1.414．

Answer 1

【答案】解：过点C作CD⊥AB垂足为D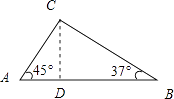
，
在Rt△ACD中，tanA=tan45°= =1，CD=AD，
sinA=sin45°= = ，AC= CD．
在Rt△BCD中，tanB=tan37°= ≈0.75，BD= ；
sinB=sin37°= ≈0.60，CB= ．
∵AD+BD=AB=63，
∴CD+ =63，
解得CD≈27，
AC= CD≈1.414×27=38.178≈38.2，
CB= ≈ =45.0，
答：AC的长约为38.2cm，CB的长约等于45.0m．
【解析】本题考查了解直角三角形的应用，利用线段的和差得出关于CD的方程是解题关键．根据锐角三角函数，可用CD表示AD，BD，AC，BC，根据线段的和差，可得关于CD的方程，根据解方程，可得CD的长，根据AC= CD，CB= ，可得答案．