Question

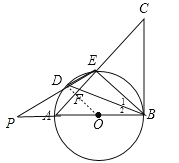
【题目】如图，AB是⊙O的直径，点D是上一点，且∠BDE=∠CBE，BD与AE交于点F．

（1）求证：BC是⊙O的切线；

（2）若BD平分∠ABE，求证：=DFDB；

（3）在（2）的条件下，延长ED、BA交于点P，若PA=AO，DE=2，求PD的长．

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）4．

【解析】

试题分析：（1）利用圆周角定理得到∠AEB=90°，∠EAB=∠BDE，而∠BDE=∠CBE，则∠CBE+∠ABE=90°，则根据切线的判定方法可判断BC是⊙O的切线；

（2）证明△DFE∽△DEB，然后利用相似比可得到结论；’

（3）连结DE，先证明OD∥BE，则可判断△POD∽△PBE，然后利用相似比可得到关于PD的方程，再解方程求出PD即可．

试题解析：（1）证明：∵AB是⊙O的直径，∴∠AEB=90°，∴∠EAB+∠ABE=90°，∵∠EAB=∠BDE，∠BDE=∠CBE，∴∠CBE+∠ABE=90°，即∠ABC=90°，∴AB⊥BC，∴BC是⊙O的切线；

（2）证明：∵BD平分∠ABE，∴∠1=∠2，而∠2=∠AED，∴∠AED=∠1，∵∠FDE=∠EDB，∴△DFE∽△DEB，∴DE：DF=DB：DE，∴=DFDB；

（3）连结DE，如图，∵OD=OB，∴∠2=∠ODB，而∠1=∠2，∴∠ODB=∠1，∴OD∥BE，∴△POD∽△PBE，∴，∵PA=AO，∴PA=AO=BO，∴，即，∴PD=4．