题目内容
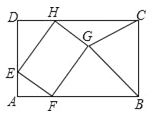
【题目】如图,矩形ABCD中,AD=6,CD=6+![]() ,E为AD上一点,且AE=2,点F,H分别在边AB,CD上,四边形EFGH为矩形,点G在矩形ABCD的内部,则当△BGC为直角三角形时,AF的值是 .
,E为AD上一点,且AE=2,点F,H分别在边AB,CD上,四边形EFGH为矩形,点G在矩形ABCD的内部,则当△BGC为直角三角形时,AF的值是 .
【答案】2或4
【解析】
试题分析:如图过点G作MN⊥AB垂足为M,交CD于N,作GK⊥BC于K.
∵四边形EFGH是矩形,
∴GH=EF,GH∥EF,∠A=90°,
∴∠DNM+∠NMA=90°,
∴∠AMN=∠DNM=90°,
∵CD∥AB,
∴∠NHG=∠AFE,
在△HNG和△FAE中,
 ,
,
∴△HNG≌△FAE,
∴AE=NG=2,ED=GM=4,
∵四边形NGKC、四边形GMBK都是矩形,
∴CK=GN=2,BK=MG=4,
当∠CGB=90°时,∵△CGK∽△GBK,
∴![]() ,
,
∴GK=MB=CN=2![]() ,
,
∴DN=AM=AB﹣MB=6,
∴四边形AMND是正方形,设AF=x,则FM=6﹣x,
∵△AEF∽△MFG,
∴![]() ,
,
∴![]()
∴x2﹣6x+8=0,
∴x=2或4.
∴AF=2或4.
故答案为2或4


练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目