题目内容
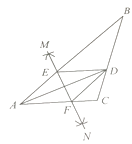
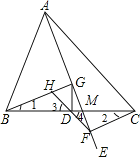
【题目】如图,在△ABC中,点D为边BC的中点,过点A作射线AE,过点C作CF⊥AE于点F,过点B作BG⊥AE于点G,连接FD并延长,交BG于点H.
(1)求证:DF=DH;
(2)若∠CFD=120°,求证:△DHG为等边三角形.

【答案】(1)证明见解析;(2)证明见解析.
【解析】试题
(1)首先证明∠1=∠2,再证明△DCF≌△DBH即可得到DF=DH;
(2)首先根据角的和差关系可以计算出∠GFH=30°,再由∠BGM=90°可得∠GHD=60°,再根据直角三角形的性质可得,HG=![]() HF,进而得到结论.
HF,进而得到结论.
试题解析:(1)∵CF⊥AE,BG⊥AE,
∴∠BGF=∠CFG=90°,
∴∠1+∠GMB=∠2+∠CME,
∵∠GMB=∠CME,
∴∠1=∠2,
∵点D为边BC的中点,
∴DB=CD,
在△BHD和△CED中,
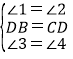
∴△BHD≌△CED(ASA),
∴DF=DH;
(2)∵∠CFD=120°,∠CFG=90°,
∴∠GFH=30°,
∵∠BGM=90°,
∴∠GHD=60°,
∵△HGF是直角三角形,HD=DF,
∴DG=![]() HF=DH,
HF=DH,
∴△DHG为等边三角形.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目