Question

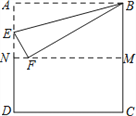
【题目】如图，把正方形纸片ABCD沿对边中点所在的直线对折后展开，折痕为MN，再过点B折叠纸片，使点A落在MN上的点F处，折痕为BE．若AB的长为2，求：

(1) FN的长；

(2) EN的长.(结果保留根号)

Answer 1

【答案】(1) ；(2) .

【解析】试题分析：（1）根据翻折不变性，AB=FB=2，BM=1，在Rt△BFM中，可利用勾股定理求出FM的值，进而可求出FN的长；

（2）根据翻折不变性，AE=EF，在Rt△EFN中，可利用勾股定理求出EF的值，

试题解析：∵四边形ABCD为正方形，AB=2，过点B折叠纸片，使点A落在MN上的点F处，

∴FB=AB=2，BM=1，

则在Rt△BMF中，

FM==，

FN=NM-FM=；

（2）设EN=x，则AE=EF=1-x，

在Rt△EFN中，由勾股定理，得EN2+ F N 2=EF2，即(1-x)2+()2=x2，

解得x=.

即EN=.