题目内容
 如图,若O是△ABC内任意一点,点D,E,F分别在OA,OB,OC上,且DE∥AB,DF∥AC,AD:DO=1:2,
如图,若O是△ABC内任意一点,点D,E,F分别在OA,OB,OC上,且DE∥AB,DF∥AC,AD:DO=1:2,(1)求证:∠BAC=∠EDF;
(2)求EF:BC的值.
分析:(1)利用平行线的性质,得∠BAD=∠EDO,∠CAD=∠FDO,故∠BAC=∠EDF;
(2)易证
=
=
,从而△FDE∽△CAB,利用对应边成比例可得EF:BC的值.
(2)易证
| DE |
| AB |
| DF |
| AC |
| 2 |
| 3 |
解答:解:(1)∵DE∥AB,
∴∠BAD=∠EDO,
又∵DF∥AC,
∴∠CAD=∠FDO,
∴∠BAD+∠CAD=∠EDO+∠FDO,即∠BAC=∠EDF.
(2)∵AD:DO=1:2,
∴OD:OA=2:3,
∵DE∥AB,DF∥AC,
∴DE:AB=OD:OA=DF:AC,
∴
=
=
,
又∵∠BAC=∠EDF,
∴△FDE∽△CAB,
∴
=
=
.
∴∠BAD=∠EDO,
又∵DF∥AC,
∴∠CAD=∠FDO,
∴∠BAD+∠CAD=∠EDO+∠FDO,即∠BAC=∠EDF.
(2)∵AD:DO=1:2,
∴OD:OA=2:3,
∵DE∥AB,DF∥AC,
∴DE:AB=OD:OA=DF:AC,
∴
| DE |
| AB |
| DF |
| AC |
| 2 |
| 3 |
又∵∠BAC=∠EDF,
∴△FDE∽△CAB,
∴
| EF |
| BC |
| DE |
| AB |
| 2 |
| 3 |
点评:本题考查了相似三角形的判定与性质,解答本题的关键是掌握相似三角形的判定定理及相似三角形对应边成比例的性质.

练习册系列答案
相关题目
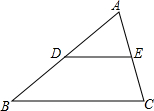 如图,若DE是△ABC的中位线,△ABC的周长为1,则△ADE的周长为( )
如图,若DE是△ABC的中位线,△ABC的周长为1,则△ADE的周长为( )| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
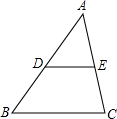 如图,若DE是△ABC的中位线,△ABC的周长为6,则△ADE的周长为( )
如图,若DE是△ABC的中位线,△ABC的周长为6,则△ADE的周长为( )| A、4 | B、3 | C、2 | D、1 |
 如图,若BD是△ABC的角平分线,则∠1=∠
如图,若BD是△ABC的角平分线,则∠1=∠