题目内容
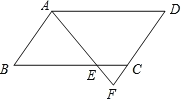
【题目】(1)问题发现:如图1,在等腰直角三角形![]() 中,
中,![]() ,将边
,将边![]() 绕点
绕点![]() 顺时针旋转90°得到线段
顺时针旋转90°得到线段![]() ,连接
,连接![]() ,则
,则![]() 的面积为__________;(请用含
的面积为__________;(请用含![]() 的式子表示
的式子表示![]() 的面积;提示:过点
的面积;提示:过点![]() 作
作![]() 边上的高
边上的高![]() )
)
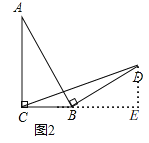
(2)类比探究:如图2,在一般的![]() 中,
中,![]() ,将边
,将边![]() 绕点
绕点![]() 顺时针旋转90°得到线段
顺时针旋转90°得到线段![]() ,连接
,连接![]() .(1)中的结论是否成立,若成立,请说明理由.
.(1)中的结论是否成立,若成立,请说明理由.
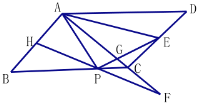
(3)拓展应用:如图3,在等腰三角形![]() 中,
中,![]() ,将边
,将边![]() 绕点
绕点![]() 顺时针旋转90°得到线段
顺时针旋转90°得到线段![]() ,连接
,连接![]() .试直接用含
.试直接用含![]() 的式子表示
的式子表示![]() 的面积.(不写探究过程)
的面积.(不写探究过程)
【答案】(1)![]() ;(2)成立,理由见解析;(3)
;(2)成立,理由见解析;(3)![]()
【解析】
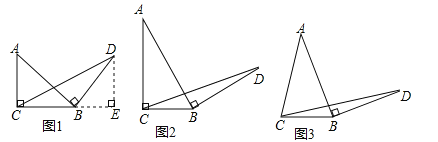
(1)如图1,过点D作BC的垂线,与BC的延长线交于点E,由垂直的性质就可以得出△ABC≌△BDE,就有DE=BC=a进而由三角形的面积公式得出结论;
(2)如图2,过点D作BC的垂线,与BC的延长线交于点E,由垂直的性质就可以得出△ABC≌△BDE,就有.DE=BC=a进而由三角形的面积公式得出结论;
(3)如图3,过点A作AF⊥BC与F,过点D作DE⊥BC的延长线于点E,由等腰三角形的性质可以得出BF= ![]() BC,由条件可以得出△AFB≌△BED就可以得出BF=DE,由三角形的面积公式就可以得出结论.
BC,由条件可以得出△AFB≌△BED就可以得出BF=DE,由三角形的面积公式就可以得出结论.
解:(1)如图1,
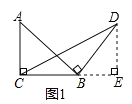
过点D作DE⊥CB交CB的延长线于E,
∴∠BED=∠ACB=90°,
由旋转知,AB=BD,∠ABD=90°,
∴∠ABC+∠DBE=90°,
∵∠A+∠ABC=90°,
∴∠A=∠DBE,
在△ABC和△BDE中,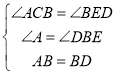 ,
,
∴△ABC≌△BDE(AAS)
∴BC=DE=a.
∵S△BCD=![]() BCDE =
BCDE =![]()
故答案为![]()
(2)(1)中结论仍然成立,
理由:如图,
过点![]() 作
作![]() 边上的高
边上的高![]() ,
,
在![]() 中,∵
中,∵![]() ,
,
由旋转可知:![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]()
(3)![]() .
.
如图3,
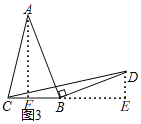
过点A作AF⊥BC与F,过点D作DE⊥BC的延长线于点E,
∴∠AFB=∠E=90°,BF=![]() BC=
BC=![]() a.
a.
∴∠FAB+∠ABF=90°
∵∠ABD=90°,
∴∠ABF+∠DBE=90°,
∴∠FAB=∠EBD
∵线段BD是由线段AB旋转得到的,
∴AB=BD
在△AFB和△BED中,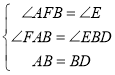 ,
,
∴△AFB≌△BED(AAS),
∴BF=DE=![]() a.
a.
∵S△BCD=![]() BCDE=
BCDE=![]()
![]() aa=
aa=![]() .
.
∴△BCD的面积为![]() .
.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案