Question

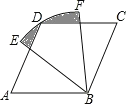
【题目】在正方形ABCD外侧作直线AP，点B关于直线AP的对称点为E，连接BE，DE，其中DE交直线AP于点F．

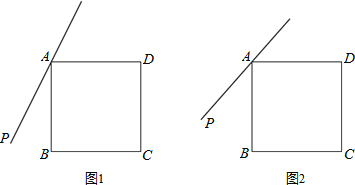
（1）依题意补全图1；

（2）若∠PAB＝20°，求∠ADF的度数；

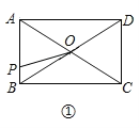
（3）如图2，若45°＜∠PAB＜90°，用等式表示线段AB，FE，FD之间的数量关系，并证明．

Answer 1

【答案】（1）见解析；（2）25°；（3）EF2+FD2＝2AB2，见解析

【解析】

（1）根据题意直接画出图形得出即可；

（2）利用对称的性质以及等角对等边进而得出答案；

（3）由轴对称的性质可得：EF＝BF，AE＝AB＝AD，∠ABF＝∠AEF＝∠ADF，进而利用勾股定理得出答案．

解：（1）如图1所示：

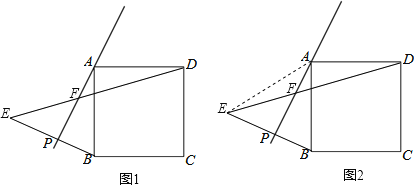
（2）如图2，连接AE，

则∠PAB＝∠PAE＝20°，AE＝AB＝AD，

∵四边形ABCD是正方形，

∴∠BAD＝90°，

又∵∠EAP＝∠BAP＝20°，

∴∠EAD＝130°，

∴；

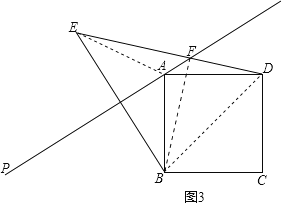
（3）数量关系是; EF2+FD2＝2AB2

如图3，连接AE、BF、BD，

由轴对称的性质和正方形的性质可得：

EF＝BF，AE＝AB＝AD，

∠ABF＝∠AEF＝∠ADF，

∴∠BFD＝∠BAD＝90°，

∴BF2+FD2＝BD2，

∵在Rt△ABD中AD2+AB2=BD2

∴EF2+FD2＝2AB2．