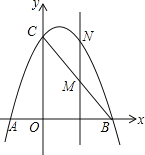
题目内容
【题目】如图,在直角坐标系内,已知![]() ,过点
,过点![]() 作互相垂直的两条直线
作互相垂直的两条直线![]() 、
、![]() ,
, ![]() 分别交
分别交![]() 轴于
轴于![]() 两点;
两点;![]() 分别交
分别交![]() 轴于
轴于![]() 两点,已知
两点,已知![]() .
.
(1)求![]() 的直线解析式;
的直线解析式;
(2)若点![]() 在
在![]() 轴的负半轴,已知抛物线
轴的负半轴,已知抛物线![]() 的对称轴经过点
的对称轴经过点![]() ,抛物线与
,抛物线与![]() 交于对称轴左侧的
交于对称轴左侧的![]() 点,当
点,当![]() 时,求抛物线的函数表达式.
时,求抛物线的函数表达式.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]()
【解析】
(1)过点![]() 作
作![]() 轴垂线,利用母子三角形的性质得到B的坐标,分情况建立图形,利用相似三角形的性质求得A的坐标可得
轴垂线,利用母子三角形的性质得到B的坐标,分情况建立图形,利用相似三角形的性质求得A的坐标可得![]() 的解析式.(2)先确定好
的解析式.(2)先确定好![]() 的解析式,利用
的解析式,利用![]() 求解
求解![]() 的解析式,确定点C的坐标,画好符合题意的图形,过M作对称轴的垂线,找到转化的相似三角形,确定好M的坐标,利用待定系数法求解解析式.
的解析式,确定点C的坐标,画好符合题意的图形,过M作对称轴的垂线,找到转化的相似三角形,确定好M的坐标,利用待定系数法求解解析式.
解:(1)过点![]() 作
作![]() 轴垂线,垂足为
轴垂线,垂足为![]() .
.![]() ,
,
![]() ,∴
,∴![]() ,设
,设![]() ,则
,则![]() ,
,
∴![]() ,解得
,解得![]() ,
,![]() ,
,
∴![]() 点坐标为
点坐标为![]() 或
或![]()
①当![]() 时,如图1,
时,如图1,![]() ,
,![]() ,因为
,因为![]() //
//![]() 轴,
轴,
所以![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,
,
所以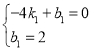 ,解得:
,解得: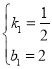 ,
,
所以![]() ;
;
②当![]() 时,如图1,
时,如图1,![]() ,
,![]() ,
,
同理:![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
同理:![]() ;
;
综上所述,![]() 的直线解析式为
的直线解析式为![]() 或
或![]() .
.
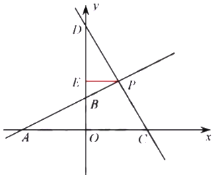
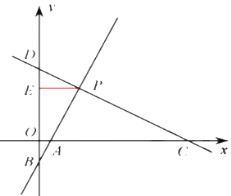
(2)当点![]() 在
在![]() 轴的负半轴时,
轴的负半轴时,![]() 的直线解析式为
的直线解析式为![]() ,因为
,因为![]() ,
,
所以![]() ,因为
,因为![]() ,所以
,所以![]()
设![]() ,把
,把![]() 代入解析式得,
代入解析式得,![]() ,
,
所以![]() ,所以
,所以![]() 点坐标为
点坐标为![]() .
.
对称轴经过点![]() ,∴对称轴
,∴对称轴![]() 为直线
为直线![]() ,
,![]() 为对称轴与
为对称轴与![]() 轴的交点,
轴的交点,
∴设解析式为![]() ,
,![]() ,
,
∴作![]() ,所以
,所以![]() ,
,
所以![]() ,
,
所以![]()
所以![]() ,
,
∴![]() .
.
解得![]() ,
,![]() ,∴
,∴![]() ,
,
∴![]() ,代入抛物线
,代入抛物线![]()
求得解析式为![]() .
.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目