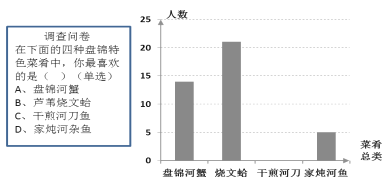
题目内容
【题目】小明和小亮在学习探索三角形全等时,碰到如下一题:如图1,若AC=AD,BC=BD,则△ACB与△ADB有怎样的关系? 


(1)请你帮他们解答,并说明理由.
(2)细心的小明在解答的过程中,发现如果在AB上任取一点E,连接CE、DE,则有CE=DE,你知道为什么吗?(如图2)
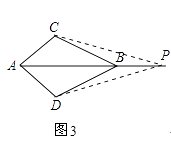
(3)小亮在小明说出理由后,提出如果在AB的延长线上任取一点P,也有第2题类似的结论.请你帮他画出图形,并写出结论,不要求说明理由.(如图3)
【答案】
(1)解:△ACB≌△ADB,理由如下:
如图1,∵在△ACB与△ADB中,
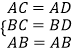 ,
,
∴△ACB≌△ADB(SSS)
(2)解:如图2,∵由(1)知,△ACB≌△ADB,则∠CAE=∠DAE.
∴在△CAE与△DAE中,
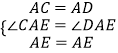 ,
,
∴△CAE≌△DAE(SAS),
∴CE=DE
(3)解:如图3,PC=PD.
理由同(2),△APC≌△APD(SAS),则PC=PD
【解析】(1)根据全等三角形的判定定理SSS证得△ACB≌△ADB;(2)由(1)中的全等三角形(△ACB≌△ADB)的对应角相等证得∠CAE=∠DAE,则由全等三角形的判定定理SAS证得△CAE≌△DAE,则对应边CE=DE;(3)同(2),利用全等三角形的对应边相等证得结论.

练习册系列答案
相关题目