题目内容
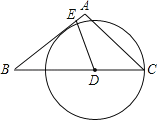
【题目】如图1,两半径为r的等圆⊙O1和⊙O2相交于M,N两点,且⊙O2过点O1.过M点作直线AB垂直于MN,分别交⊙O1和⊙O2于A,B两点,连接NA,NB.
(1)猜想点O2与⊙O1有什么位置关系,并给出证明;
(2)猜想△NAB的形状,并给出证明;
(3)如图2,若过M的点所在的直线AB不垂直于MN,且点A,B在点M的两侧,那么(2)中的结论是否成立,若成立请给出证明.
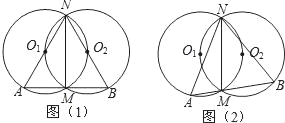
【答案】(1)O2在⊙O1上(2)△NAB是等边三角形(3)仍然成立
【解析】试题分析:(1)通过证明圆心距等于半径得出点![]() 在
在![]() 上;
上;
(2)通过证明![]() 从而得到
从而得到![]() 是等边三角形;
是等边三角形;
(3)根据在同圆中等弧所对的圆周角相等,可求出![]() 从求证得
从求证得![]() 是等边三角形.
是等边三角形.
试题解析:(1) ![]() 在
在![]() 上,
上,
证明:∵![]() 过点
过点![]() ,
,
![]()
又∵![]() 的半径也是r,
的半径也是r,
∴点![]() 在
在![]() 上;
上;
(2)△NAB是等边三角形,
证明:∵MN⊥AB,
![]()
∴BN是的直径,AN是![]() 的直径,
的直径,
即BN=AN=2r, ![]() 在BN上,
在BN上, ![]() 在AN上.
在AN上.
连接![]() ,则
,则![]() 是△ABN的中位线。
是△ABN的中位线。
![]()
∴AB=BN=AN,则△NAB是等边三角形.
(3)仍然成立.
证明:由(2)得,△NAB是等边三角形,
∴在![]() 中,
中, ![]() 所对的圆周角为
所对的圆周角为![]() ,在
,在![]() 中
中![]() 所对的圆周角为
所对的圆周角为![]() ,
,
∴当点A,B在点M的两侧时,
在![]() 中
中![]() 所对的圆周角
所对的圆周角![]()
在![]() 中
中![]() 所对的圆周角
所对的圆周角![]()
∴△NAB是等边三角形.
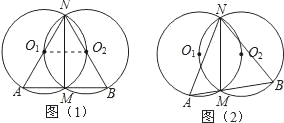

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目