题目内容
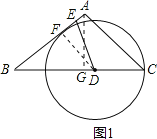
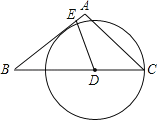
【题目】如图,在等腰△ABC中,AB=AC=5,BC=6,点D为BC边上一动点(不与点B重合),过D作射线DE交AB边于E,使∠BDE=∠A,以D为圆心、DC的长为半径作⊙D.
(1)设BD=x,AE=y,求y关于x的函数关系式,并写出定义域.
(2)当⊙D与AB边相切时,求BD的长.
(3)如果⊙E是以E为圆心,AE的长为半径的圆,那么当BD的长为多少时,⊙D与⊙E相切?
【答案】(1) y=5-![]() x(0<x≤
x(0<x≤![]() );(2)
);(2) ![]() ;(3)
;(3) ![]() 或
或![]() .
.
【解析】
试题分析:(1)通过相似三角形△BDE∽△BAC的对应边成比例得到![]() ,把相关线段的长度代入并整理得到y=5-
,把相关线段的长度代入并整理得到y=5-![]() x(0<x≤
x(0<x≤![]() );
);
(2)如图,假设AB与⊙D相切于点F,连接FD.通过相似三角形△BFD∽△BGA的对应边成比例得到![]() .DF=6-BD,由勾股定理求得AG=4,BA=5,所以把相关线段的长度代入便可以求得BD的长度;
.DF=6-BD,由勾股定理求得AG=4,BA=5,所以把相关线段的长度代入便可以求得BD的长度;
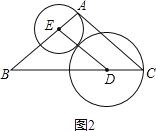
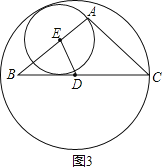
(3)分类讨论:⊙D与⊙E相外切和内切两种情况.由(1)的相似三角形推知BD=ED.所以如图2,当⊙D与⊙E相外切时.AE+CD=DE=BD;如图3,当⊙D与⊙E相内切时.CD-AE=DE=BD.
试题解析:(1)如图,∵∠B=∠B,∠BDE=∠A,
∴△BDE∽△BAC,
∴![]() ,
,
∵AB=AC=5,BC=6,BD=x,AE=y,
∴![]() ,即y=5-
,即y=5-![]() x.
x.
∵0<x≤6,且0≤y≤5,
∴0<x≤![]() .
.
综上所述,y关于x的函数关系式及其定义域为:y=5-![]() x(0<x≤
x(0<x≤![]() );
);
(2)如图,假设AB与⊙D相切于点F,连接FD,则DF=DC,∠BFD=90°.
过点A作AG⊥BC于点G,则∠BGA=90°.
∴在△BFD和△BGA中,∠BFD=∠BGA=90°,∠B=∠B,
∴△BFD∽△BGA,
∴![]() .
.
又∵AB=AC=5,BC=6,AG⊥BC
∴BG=![]() ,AG=
,AG=![]() ,
,
∴![]() ,解得BD=
,解得BD=![]() ;
;
(3)∵由(1)知,△BDE∽△BAC,
∴![]() ,即
,即![]() ,
,
∴BD=DE.
如图2,当⊙D与⊙E相外切时.
AE+CD=DE=BD,
∵由(1)知,BD=x,AE=y,y关于x的函数关系式是y=5-![]() x,
x,
∴5-![]() x+6-x=x,
x+6-x=x,
解得,x=![]() ,符合0<x≤
,符合0<x≤![]() ,
,
∴BD的长度为![]() .
.
如图3,当⊙D与⊙E相内切时.CD-AE=DE=BD,
∵由(1)知,BD=x,AE=y,y关于x的函数关系式是y=5-![]() x,
x,
∴6-x-5+![]() x=x,
x=x,
解得,x=![]() ,符合0<x≤
,符合0<x≤![]() ,
,
∴BD的长度为![]() .
.
综上所述,BD的长度是![]() 或
或![]() .
.