Question

【题目】如图1，点O为直线AB上一点，过点O作射线OC，使∠BOC＝120°．将一直角三角板的直角顶点放在点O处，一边OM在射线OB上，另一边ON在直线AB的下方．将图1中的三角板绕点O逆时针旋转至图2，使一边OM在∠BOC的内部，另一边ON仍在直线AB的下方．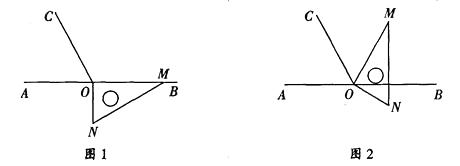

（1）若OM恰好平分∠BOC，求∠BON的度数；
（2）若∠BOM等于∠COM余角的3倍，求∠BOM的度数；
（3）若设∠BON＝α（0°<α<90°），试用含α的代数式表示∠COM．

Answer 1

【答案】
（1）解： ∵∠BOC=120° ，OM恰好平分 ∠BOC
∴∠BOM=∠BOC=60°
又 ∵∠MON=90°
∴∠BON=∠MON∠BOM
=90°60°=30°

（2）解：设 的余角为x°，
则
由题意得： ，
x=15,
3x=45，
所以 的度数为45°
（3）解： （0°< <90°）．

．

【解析】（1）利用角平分线的定义求出∠BOM的度数，再根据∠BON=∠MON∠BOM，即可求出结果。
（2）设∠ C O M 的余角为x°，表示出∠COM的度数，再根据∠BOM=∠COM余角的3倍，建立方程求解即可。
（3）根据角的和与差计算即可。
【考点精析】通过灵活运用角的平分线和图形的旋转，掌握从一个角的顶点引出的一条射线，把这个角分成两个相等的角，这条射线叫做这个角的平分线；每一个点都绕旋转中心沿相同方向转动了相同的角度，任意一对对应点与旋转中心的连线所成的角都是旋转角，对应点到旋转中心的距离相等．旋转的方向、角度、旋转中心是它的三要素即可以解答此题．