题目内容
P是∠AOB内一点,分别作点P关于直线OA、OB的对称点P1、P2,连接OP1、OP2,则下列结论正确的是
A.OP1⊥OP2 B.OP1=OP2 C.OP1⊥OP2且OP1=OP2 D.OP1≠OP2
A.OP1⊥OP2 B.OP1=OP2 C.OP1⊥OP2且OP1=OP2 D.OP1≠OP2
B
试题分析:如图,∵点P关于直线OA、OB的对称点P1、P2,

∴OP1=OP2=OP,∠AOP=∠AOP1,∠BOP=∠BOP2。
∴∠P1OP2=∠AOP+∠AOP1+∠BOP+∠BOP2=2(∠AOP+∠BOP)=2∠AOB。
∵∠AOB度数任意,∴OP1⊥OP2不一定成立。
故选B。

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目













 和3的两个正方形放置在直线l上,如图1,他连结AD、CF,经测量发现AD=CF.
和3的两个正方形放置在直线l上,如图1,他连结AD、CF,经测量发现AD=CF.
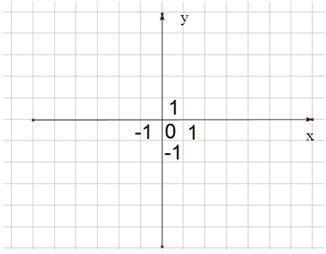
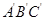 ,画出△
,画出△