题目内容
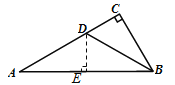
【题目】如图,在△ABC中,∠C=90°, ∠ABC=60°,BD平分∠ABC,若AD=6,则AC= .
【答案】9.
【解析】试题分析:根据角平分线的定义求得∠2=∠3=30°,从而求得直角三角形BCD的直角边CD是斜边BD长度的一半;然后由三角形的外角定理知∠4=∠1+∠2,所以∠1=∠2=30°,根据等角对等边可知AD=BD;最后根据图示、等量代换求得AC=![]() AD=9.
AD=9.
试题解析:∵△ABC中,∠C=90°,∠ABC=60°,BD平分∠ABC,
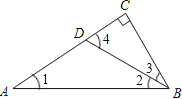
∴∠2=∠3=30°;
在Rt△BCD中,
CD=![]() BD,∠4=90°-30°=60°(直角三角形的两个锐角互余);
BD,∠4=90°-30°=60°(直角三角形的两个锐角互余);
∴∠1+∠2=60°(外角定理),
∴∠1=∠2=30°,
∴AD=BD(等角对等边);
∴AC=AD+CD=![]() AD;
AD;
又∵AD=6,
∴AC=9.

练习册系列答案
相关题目