题目内容
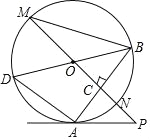
【题目】如图,已知⊙O中,AB为弦,直线PO交⊙O于点M、N,PO⊥AB于C,过点B作直径BD,连接AD、BM、AP.
(1)求证:PM∥AD;
(2)若∠BAP=2∠M,求证:PA是⊙O的切线;
(3)若AD=6,tan∠M=![]() ,求⊙O的直径.
,求⊙O的直径.
【答案】(1)证明见解析;(2)证明见解析;(3)5;
【解析】
(1)根据平行线的判定求出即可;(2)连接OA,求出∠OAP=∠BAP+∠OAB=∠BOC+∠OBC=90°,根据切线的判定得出即可;(3)设BC=x,CM=2x,根据相似三角形的性质和判定求出NC=![]() x,求出MN=2x+
x,求出MN=2x+![]() x=2.5x,OM=
x=2.5x,OM=![]() MN=1.25x,OC=0.75x,根据三角形的中位线性质得出0.75x=
MN=1.25x,OC=0.75x,根据三角形的中位线性质得出0.75x=![]() AD=3,求出x即可.
AD=3,求出x即可.
(1)∵BD是直径,
∴∠DAB=90°,
∵PO⊥AB,
∴∠DAB=∠MCB=90°,
∴PM∥AD;
(2)连接OA,
∵OB=OM,
∴∠M=∠OBM,
∴∠BON=2∠M,
∵∠BAP=2∠M,
∴∠BON=∠BAP,
∵PO⊥AB,
∴∠ACO=90°,
∴∠AON+∠OAC=90°,
∵OA=OB,
∴∠BON=∠AON,
∴∠BAP=∠AON,
∴∠BAP+∠OAC=90°,
∴∠OAP=90°,
∵OA是半径,
∴PA是⊙O的切线;
(3)连接BN,
则∠MBN=90°.
∵tan∠M=![]() ,
,
∴![]() =
=![]() ,
,
设BC=x,CM=2x,
∵MN是⊙O直径,NM⊥AB,
∴∠MBN=∠BCN=∠BCM=90°,
∴∠NBC=∠M=90°﹣∠BNC,
∴△MBC∽△BNC,
∴![]() ,
,
∴BC2=NC×MC,
∴NC=![]() x,
x,
∴MN=2x+![]() x=2.5x,
x=2.5x,
∴OM=![]() MN=1.25x,
MN=1.25x,
∴OC=2x﹣1.25x=0.75x,
∵O是BD的中点,C是AB的中点,AD=6,
∴OC=0.75x=![]() AD=3,
AD=3,
解得:x=4,
∴MO=1.25x=1.25×4=5,
∴⊙O的半径为5.