题目内容
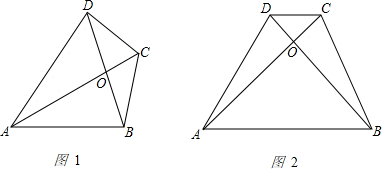
(1)如图1,四边形ABCD中,对角线AC、BD相交于点O,若△AOB的面积为S1,△BOC的面积为S2,△COD的面积为S3,△AOD的面积为S4 ,求证:S1S3=S2S4;
(2)如图2,四边形ABCD是梯形,对角线AC、BD相交于点O,若△AOB的面积为4,△BOC的面积为9,求梯形ABCD的面积.
解:(1)作BE⊥AC于点E,

则
∴ ,
,
同理可证: ,
,
∴
∴S1S3=S2S4;
(2)∵AB∥CD,
∴S△ABD=S△ABC(同底等高)
∴S△AOD=S△BOC,
设AOD的面积为S,
由(1)可得S2=4×9
∴S=6,
∴梯形ABCD的面积=6+6+4+9=25.
分析:(1)作BE⊥AC于点E,从而可分别表示出S1和S2然后可得出 ,同理可得出
,同理可得出 ,这样即可证得结论.
,这样即可证得结论.
(2)根据同底等高的三角形的面积相等可得出S△ABD=S△ABC,S△AOD=S△BOC,从而解出AOD的面积,也就能得出梯形的面积.
点评:本题考查梯形及三角形的面积,难度一般,对于此类综合性题目,同学们首要做的还是掌握基本概念,只有这样才能在解答综合题时融会贯通.

则

∴
 ,
,同理可证:
 ,
,∴

∴S1S3=S2S4;
(2)∵AB∥CD,
∴S△ABD=S△ABC(同底等高)
∴S△AOD=S△BOC,
设AOD的面积为S,
由(1)可得S2=4×9
∴S=6,
∴梯形ABCD的面积=6+6+4+9=25.
分析:(1)作BE⊥AC于点E,从而可分别表示出S1和S2然后可得出
 ,同理可得出
,同理可得出 ,这样即可证得结论.
,这样即可证得结论.(2)根据同底等高的三角形的面积相等可得出S△ABD=S△ABC,S△AOD=S△BOC,从而解出AOD的面积,也就能得出梯形的面积.
点评:本题考查梯形及三角形的面积,难度一般,对于此类综合性题目,同学们首要做的还是掌握基本概念,只有这样才能在解答综合题时融会贯通.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,在四边形ABCD中(AB≠BC),AB∥CD,AB=CD,直线EF经过四边形ABCD的对角线AC和BD的交点O,且分别交AD、BC于点M、N,交BA、DC的延长线于点E、F,下列结论:
如图,在四边形ABCD中(AB≠BC),AB∥CD,AB=CD,直线EF经过四边形ABCD的对角线AC和BD的交点O,且分别交AD、BC于点M、N,交BA、DC的延长线于点E、F,下列结论: 如图,平行四边形ABCD的对角线AC与BD相交于点O,点E、F在对角线AC上,且AF=CE.试问BE∥FD吗?说说你的理由.
如图,平行四边形ABCD的对角线AC与BD相交于点O,点E、F在对角线AC上,且AF=CE.试问BE∥FD吗?说说你的理由.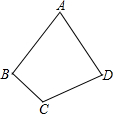 如图是一块四边形的薄钢板,∠A=60°,∠C=120°,AB=AD.
如图是一块四边形的薄钢板,∠A=60°,∠C=120°,AB=AD.
 如图,凸四边形有
如图,凸四边形有