题目内容
【题目】如图，在△ABC中，AB＝AC ， 点D（不与点B重合）在BC上，点E是AB的中点，过点A作AF∥BC交DE延长线于点F ， 连接AD ， BF ．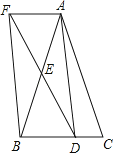 
（1）求证：△AEF≌△BED；
（2）若BD＝CD ， 求证：四边形AFBD是矩形．
【答案】
（1）
解答：证明：∵AF∥BC，∴∠AFE＝∠EDB，∵E为AB的中点，∴EA＝EB，在△AEF和△BED中，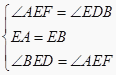 
，∴△AEF≌△BED（ASA）．
（2）
解答：证明：∵△AEF≌△BED，∴AF＝BD，∵AF∥BD，∴四边形AFBD是平行四边形，∵AB＝AC，BD＝CD，∴AD⊥BD，∴四边形AFBD是矩形．
【解析】（1）AAS或ASA证全等；（2）根据对角线互相平分的证明四边形AFBD是平行四边形，再根据等腰三角形三线合一证明∠ADB＝90°，进而根据有一个角是直角的平行四边形是矩形得证．
【考点精析】掌握矩形的判定方法是解答本题的根本，需要知道有一个角是直角的平行四边形叫做矩形；有三个角是直角的四边形是矩形；两条对角线相等的平行四边形是矩形．
练习册系列答案
阅读快车系列答案
相关题目
