题目内容
如图5,一张矩形纸片ABCD的边长分别为9cm和3cm,把![]() 顶点A和C叠合在一起,得到折痕EF.
顶点A和C叠合在一起,得到折痕EF.
(1)证明四边形AECF是菱形;
(2)计算折痕EF的长;
(3)求△CEH的面积.
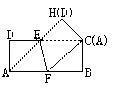
(1)如图1,因为AB∥CD,所以AF∥CE,CF∥HE,根据对称性,知∠CEH=∠AED,因为D、E、C三点共线,所以A、E、H三点共线,所以AE∥CF,所以四边形AECF是平行四边形.又AF=CF, 所以四边形AECF是菱形.
(2)设AF=x,则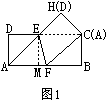
CF=x,BF=9-x.
在△BCF中,CF2=BF2+BC2,
所以x2=(9-x)2+32,
解得x=5,即CF=5,BF=![]() 4.
4.
过E作EM⊥AB交AB于M,则
MF=BM-BF=CE-BF=CF-BF=1,
EM=3.
所以![]() .
.
(3)根据对称性,知△CEH≌△AED,
所以S△CEH=S△AED=![]() DE·AD=
DE·AD=![]() (AF-MF)·AD=
(AF-MF)·AD=![]() ×4×3=6(cm2).
×4×3=6(cm2).

练习册系列答案
相关题目
 9、如图:将一张矩形纸片ABCD的角C沿着GF折叠(F在BC边上,不与B、C重合)使得C点落在矩形ABCD内部的E处,FH平分∠BFE,则∠GFH的度数α满足( )
9、如图:将一张矩形纸片ABCD的角C沿着GF折叠(F在BC边上,不与B、C重合)使得C点落在矩形ABCD内部的E处,FH平分∠BFE,则∠GFH的度数α满足( ) (2013•吉安模拟)如图,有一张矩形纸片ABCD,已知AB=2,BC=4,若点E是AD上的一个动点(与点A不重合),且0<AE≤2,沿BE将△ABE对折后,点A落到点P处,连接PC.
(2013•吉安模拟)如图,有一张矩形纸片ABCD,已知AB=2,BC=4,若点E是AD上的一个动点(与点A不重合),且0<AE≤2,沿BE将△ABE对折后,点A落到点P处,连接PC. 如图,将一张矩形纸片ABCD沿CE折叠,B点恰好落在AD边上,设此点为F,若AB:BC=4:5,则CD:DF的值是
如图,将一张矩形纸片ABCD沿CE折叠,B点恰好落在AD边上,设此点为F,若AB:BC=4:5,则CD:DF的值是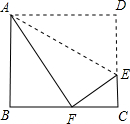 如图,将一张矩形纸片沿着AE折叠后,D点恰好落在BC边上的F上,已知AB=8cm,BC=10cm,求EC的长度.
如图,将一张矩形纸片沿着AE折叠后,D点恰好落在BC边上的F上,已知AB=8cm,BC=10cm,求EC的长度.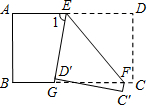 如图,把一张矩形纸片ABCD沿EF折叠后,点C、D分别落在C′、D′的位置上,ED′的延长线与BC的交点为G,若∠EFG=50°,那么∠1=
如图,把一张矩形纸片ABCD沿EF折叠后,点C、D分别落在C′、D′的位置上,ED′的延长线与BC的交点为G,若∠EFG=50°,那么∠1=