题目内容
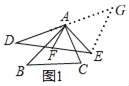
【题目】我们定义:如果两个三角形的两组对应边相等,且它们的夹角互补,我们就把其中一个三角形叫做另一个三角形的“夹补三角形”,同时把第三边的中线叫做“夹补中线.例如:图1中,△ABC与△ADE的对应边AB=AD,AC=AE,∠BAC+∠DAE=180°,AF是DE边的中线,则△ADE就是△ABC的“夹补三角形”,AF叫做△ABC的“夹补中线”.

特例感知:
(1)如图2、图3中,△ABC与△ADE是一对“夹补三角形”,AF是△ABC的“夹补中线”;
①当△ABC是一个等边三角形时,AF与BC的数量关系是: ;
②如图3当△ABC是直角三角形时,∠BAC=90°,BC=a时,则AF的长是 ;
猜想论证:
(2)在图1中,当△ABC为任意三角形时,猜想AF与BC的关系,并给予证明.
拓展应用:
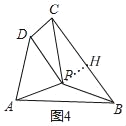
(3)如图4,在四边形ABCD中,∠DCB=90°,∠ADC=150°,BC=2AD=6,CD=![]() ,若△PAD是等边三角形,求证:△PCD是△PBA的“夹补三角形”,并求出它们的“夹补中线”的长.
,若△PAD是等边三角形,求证:△PCD是△PBA的“夹补三角形”,并求出它们的“夹补中线”的长.
【答案】(1)AF=![]() BC;
BC;![]() a;(2)猜想:AF=
a;(2)猜想:AF=![]() BC,(3)
BC,(3)![]()
【解析】
(1)①先判断出AD=AE=AB=AC,∠DAE=120°,进而判断出∠ADE=30°,再利用含30度角的直角三角形的性质即可得出结论;
②先判断出△ABC≌△ADE,利用直角三角形的性质即可得出结论;
(2)先判断出△AEG≌△ACB,得出EG=BC,再判断出DF=EF,即可得出结论;
(3)先判断出四边形PHCD是矩形,进而判断出∠DPC=30°,再判断出PB=PC,进而求出∠APB=150°,即可利用“夹补三角形”即可得出结论.
解:(1)
∵△ABC与△ADE是一对“夹补三角形”,
∴AB=AD,AC=AE,∠BAC+∠DAE=180°,
①∵△ABC是等边三角形,
∴AB=AC=BC,∠BAC=60°
∴AD=AE=AB=AC,∠DAE=120°,
∴∠ADE=30°,
∵AF是“夹补中线”,
∴DF=EF,
∴AF⊥DE,
在Rt△ADF中,AF=![]() AD=
AD=![]() AB=
AB=![]() BC,
BC,
故答案为:AF=![]() BC;
BC;
②当△ABC是直角三角形时,∠BAC=90°,
∵∠DAE=90°=∠BAC,
易证,△ABC≌△ADE,
∴DE=BC,
∵AF是“夹补中线”,
∴DF=EF,
∴AF=![]() DE=
DE=![]() BC=
BC=![]() a,
a,
故答案为![]() a;
a;
(2)解:猜想:AF=![]() BC,
BC,
理由:如图1,延长DA到G,使AG=AD,连EG
∵△ABC与△ADE是一对“夹补三角形”,
∴AB=AD,AC=AE,∠BAC+∠DAE=180°,
∴AG=AB,∠EAG=∠BAC,AE=AC,
∴△AEG≌△ACB,
∴EG=BC,
∵AF是“夹补中线”,
∴DF=EF,
∴AF=![]() EG,
EG,
∴AF=![]() BC;
BC;
(3)证明:如图4,
∵△PAD是等边三角形,
∴DP=AD=3,∠ADP=∠APD=60°,
∵∠ADC=150°,
∴∠PDC=90°,
作PH⊥BC于H,
∵∠BCD=90°
∴四边形PHCD是矩形,
∴CH=PD=3,
∴BH=6﹣3=3=CH,
∴PC=PB,
在Rt△PCD中,tan∠DPC=![]() ,
,
∴∠DPC=30°
∴∠CPH=∠BPH=60°,∠APB=360°﹣∠APD﹣∠DPC﹣∠BPC=150°,
∴∠APB+∠CPD=180°,
∵DP=AP,PC=PB,
∴△PCD是△PBA的“夹补三角形”,
由(2)知,![]() CD=
CD=![]() ,
,
∴△PAB的“夹补中线”=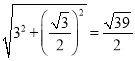 .
.

【题目】为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表.

调查结果统计表
组别 | 分组 | 人数 |
A |
| 4 |
B |
| 16 |
C |
| a |
D |
| b |
E |
| 2 |
请根据以上图表,解答下列问题:
![]() 填空:这次被调查的同学共有______ 人,
填空:这次被调查的同学共有______ 人, ![]() ______ ,
______ , ![]() ______ ;
______ ;
![]() 求扇形统计图中扇形C的圆心角度数;
求扇形统计图中扇形C的圆心角度数;
![]() 该校共有学生1000人,请估计每月零花钱的数额x在
该校共有学生1000人,请估计每月零花钱的数额x在![]() 范围的人数.
范围的人数.