题目内容
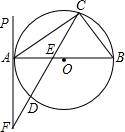 如图,△ABC内接于⊙O,AB是⊙O的直径,PA是过A点的直线,∠PAC=∠B,
如图,△ABC内接于⊙O,AB是⊙O的直径,PA是过A点的直线,∠PAC=∠B,(1)求证:PA是⊙O的切线;
(2)如果弦CD交AB于E,CD的延长线交PA于F,AC=8,CE:ED=6:5,AE:EB=2:3,求AB的长和∠ECB的正切值.
分析:(1)要证PA是⊙O的切线,只要证∠PAO=90°即可,因为AB为直径,所以有∠CAB+∠CBA=90°,又∠PAC=∠B,所以∠CAB+∠PAC=90°即PA是⊙O的切线.
(2)连接AD、BD;可设CE=6x,AE=2y,进而根据已知条件,用x、y表示出DE、BE的长,由相交弦定理,即可求得x、y的比例关系;易证得△AEC∽△BED,根据所得成比例线段,即可求得BD的长,同理可设BC=m,由△BEC∽△DEA,求得AD的表达式;在Rt△ADB和Rt△ACB中,可由勾股定理分别表示出AB2,即可得到关于m的方程,从而求出m的值,即BC的长,即可由勾股定理求得AB的长;
根据圆周角定理知:∠ECB=∠DAB,因此只需在Rt△ABD中,求出∠DAB的正切值即可.
(2)连接AD、BD;可设CE=6x,AE=2y,进而根据已知条件,用x、y表示出DE、BE的长,由相交弦定理,即可求得x、y的比例关系;易证得△AEC∽△BED,根据所得成比例线段,即可求得BD的长,同理可设BC=m,由△BEC∽△DEA,求得AD的表达式;在Rt△ADB和Rt△ACB中,可由勾股定理分别表示出AB2,即可得到关于m的方程,从而求出m的值,即BC的长,即可由勾股定理求得AB的长;
根据圆周角定理知:∠ECB=∠DAB,因此只需在Rt△ABD中,求出∠DAB的正切值即可.
解答: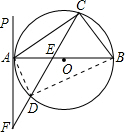 (1)证明:∵AB是⊙O的直径,
(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°;
∴∠CAB+∠CBA=90°;
又∠PAC=∠B,
∴∠CAB+∠PAC=90°;
∴∠PAB=90°;
即PA是⊙O的切线.
(2)解:设CE=6x,AE=2y,则DE=5x,BE=3y;
由相交弦定理,得:AE•EB=CE•DE,即:
2y•3y=5x•6x,解得:
x=y;
∵∠ACD=∠ABD,∠AEC=∠DEB,
∴△AEC∽△DEB,则有:
=
;
∵AE=2y=2
x,DE=5x,
∴
=
,由于AC=8,则BD=4
;
设BC=m,同理可求得AD=
m;
∵AB是直径,∴△ACB、△ADB是直角三角形;
由勾股定理,得:AB2=AC2+BC2=AD2+BD2,即:
82+m2=(
m)2+(4
)2,解得m=6;
故BC=6,AD=2
;
∴AB=
=10,tan∠ECB=tan∠DAB=
=2.
 (1)证明:∵AB是⊙O的直径,
(1)证明:∵AB是⊙O的直径,∴∠ACB=90°;
∴∠CAB+∠CBA=90°;
又∠PAC=∠B,
∴∠CAB+∠PAC=90°;
∴∠PAB=90°;
即PA是⊙O的切线.
(2)解:设CE=6x,AE=2y,则DE=5x,BE=3y;
由相交弦定理,得:AE•EB=CE•DE,即:
2y•3y=5x•6x,解得:
| 5 |
∵∠ACD=∠ABD,∠AEC=∠DEB,
∴△AEC∽△DEB,则有:
| AC |
| BD |
| AE |
| DE |
∵AE=2y=2
| 5 |
∴
| AC |
| BD |
2
| ||
| 5 |
| 5 |
设BC=m,同理可求得AD=
| ||
| 3 |
∵AB是直径,∴△ACB、△ADB是直角三角形;
由勾股定理,得:AB2=AC2+BC2=AD2+BD2,即:
82+m2=(
| ||
| 3 |
| 5 |
故BC=6,AD=2
| 5 |
∴AB=
| AC2+BC2 |
| BD |
| AD |
点评:本题考查了切线的判定、勾股定理、圆周角定理以及相似三角形的判定和性质等重要知识;此题的难点在于(2)题,通过两步相似来求得BD的长以及AD、BC的比例关系,是解答此题的关键.

练习册系列答案
相关题目
 15、如图,△ABC内接于⊙O,∠BAC=120°,AB=AC=4.BD为⊙O的直径,则BD=
15、如图,△ABC内接于⊙O,∠BAC=120°,AB=AC=4.BD为⊙O的直径,则BD= 21、如图,△ABC内接于⊙O,AB为⊙O的直径,点D在AB的延长线上,∠A=∠D=30°.
21、如图,△ABC内接于⊙O,AB为⊙O的直径,点D在AB的延长线上,∠A=∠D=30°.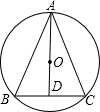 已知:如图,△ABC内接于⊙O,连接AO并延长交BC于点D,若AO=5,BC=8,∠ADB=90°,求△ABC的面积.
已知:如图,△ABC内接于⊙O,连接AO并延长交BC于点D,若AO=5,BC=8,∠ADB=90°,求△ABC的面积. 18、如图,△ABC内接于⊙O,∠A=30°,若BC=4cm,则⊙O的直径为( )
18、如图,△ABC内接于⊙O,∠A=30°,若BC=4cm,则⊙O的直径为( )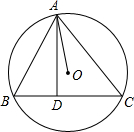 如图,△ABC内接于⊙O,AD⊥BC于点D,求证:∠BAD=∠CAO.
如图,△ABC内接于⊙O,AD⊥BC于点D,求证:∠BAD=∠CAO.