题目内容
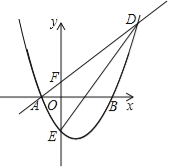
【题目】在平面直角坐标系中,将二次函数y=a![]() (a>0)的图象向右平移1个单位,再向下平移2个单位,得到如图所示的抛物线,该抛物线与x轴交于点A、B(点A在点B的左侧),OA=1,经过点A的一次函数
(a>0)的图象向右平移1个单位,再向下平移2个单位,得到如图所示的抛物线,该抛物线与x轴交于点A、B(点A在点B的左侧),OA=1,经过点A的一次函数![]() (
(![]() )的图象与y轴正半轴交于点C,且与抛物线的另一个交点为D,△ABD的面积为5.
)的图象与y轴正半轴交于点C,且与抛物线的另一个交点为D,△ABD的面积为5.
(1)求抛物线和一次函数的解析式;
(2)抛物线上的动点E在一次函数的图象下方,求△ACE面积的最大值,并求出此时点E的坐标;
【答案】(1)![]() ,
,![]() ;(2)最大值是
;(2)最大值是![]() ,此时E点坐标为
,此时E点坐标为![]()
【解析】
(1)先写出平移后的抛物线解析式,经过点A(-1,0),可求得a的值,由△ABD的面积为5可求出点D的纵坐标,代入抛物线解析式求出横坐标,由A、D的坐标可求出一次函数解析式;
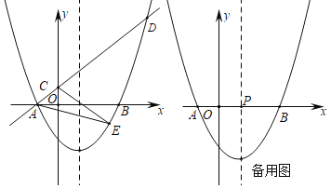
(2)作EM∥y轴交AD于M,如图,利用三角形面积公式,由![]() 构建二次函数,利用二次函数的性质即可解决问题;
构建二次函数,利用二次函数的性质即可解决问题;
(1)将二次函数![]() )的图象向右平移1个单位,再向下平移2个单位,得到的抛物线解析式为
)的图象向右平移1个单位,再向下平移2个单位,得到的抛物线解析式为![]() ,
,
∵OA=1,
∴点A的坐标为(﹣1,0),代入抛物线的解析式得,![]() ,
,
∴![]() ,
,
∴抛物线的解析式为![]() ,即
,即![]() .
.
令y=0,解得![]() ,
,
∴点B的坐标为(3,0),
∴AB=OA+OB=4,
∵△ABD的面积为5,
∴![]() ,
,
∴![]() ,
,
代入抛物线解析式得,![]() ,
,
解得![]() ,
,
∴点D的坐标为(4,![]() ),
),
设直线AD的解析式为![]() ,
,
∴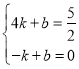 ,解得:
,解得:![]() ,
,
∴直线AD的解析式为![]() ;
;
(2)过点E作EM∥y轴交AD于M,交x轴于N,如图,
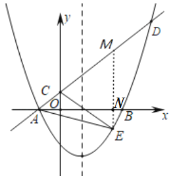
设点E的坐标为(![]() ,
,![]() ),则点M的坐标为(
),则点M的坐标为(![]() ,
,![]() )
)
∴![]() ,
,
∴![]()
![]()
![]()
![]()
![]() ,
,
∴当![]() 时,△ACE的面积有最大值,最大值是
时,△ACE的面积有最大值,最大值是![]() ,此时E点坐标为(
,此时E点坐标为( ![]() ,
,![]() )
)

【题目】甲、乙两超市(大型商场)同时开业,为了吸引顾客,都举行有奖酬宾活动:凡购物满![]() 元,均可得到一次摸奖的机会.在一个纸盒里装有
元,均可得到一次摸奖的机会.在一个纸盒里装有![]() 个红球和
个红球和![]() 个白球(编号分别为红1、红
个白球(编号分别为红1、红![]() 、白1、白
、白1、白![]() ),除颜色外其它都相同,摸奖者一次从中摸出两个球,根据球的颜色决定送礼金券(在他们超市使用时,与人民币等值)的多少(如表)
),除颜色外其它都相同,摸奖者一次从中摸出两个球,根据球的颜色决定送礼金券(在他们超市使用时,与人民币等值)的多少(如表)
甲超市:
球 | 两红 | --红一白 | 两白 |
礼金券(元) |
|
|
|
乙超市:
球 | 两红 | --红一白 | 两白 |
礼金券(元) |
|
|
|
(1)列举出一次摸奖时两球的所有情况;
(2)如果只考虑中奖因素,你将会选择去哪个超市购物?请说明理由.