题目内容
【题目】在△ABC中,AB=AC,∠A=60°,点D是线段BC的中点,∠EDF=120°,DE与线段AB相交于点E,DF与线段AC(或AC的延长线)相交于点F.
(1)如图(1)所示,若DF⊥AC,垂足为F,AB=4,求BE的长;
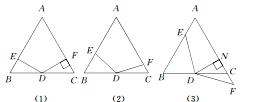
(2)如图(2)所示,将(1)中的∠EDF绕点D顺时针旋转一定的角度,DF仍与线段AC相交于点F,求证:BE+CF=![]() AB;
AB;
(3)如图(3)所示,将(2)中的∠EDF继续绕点D顺时针旋转一定的角度,使DF与线段AC的延长线交于点F,作DN⊥AC于点N,若DN=FN,求证:BE+CF=![]() (BE-CF).
(BE-CF).
【答案】(1)BE=1;(2)详见解析;(3)详见解析.
【解析】试题分析:(1)根据四边形的内角和定理得出DE⊥AB,从而得到BE的长度;
(2)取AB得中点G,连接DG,得出DG为△ABC的中位线,则DG=DC,∠BGD=∠C=60°,根据四边形对角互补得出∠GED=∠DFC,从而得到△DEG≌△DFC,得到BG=CF,得出答案;
(3)取AB得中点G,连接DG,同(2),易证△DEG≌△DFC,得出EG=CF,设CN=x,根据Rt△DCN得出CD=2x,DN=![]() x,根据题意得出EG、BE与x的关系,从而进行证明.
x,根据题意得出EG、BE与x的关系,从而进行证明.
试题解析:(1)由四边形AEDF的内角和为360°,可知DE⊥AB,故BE=2
(2)取AB的中点G,连接DG
易证:DG为△ABC的中位线,故DG=DC,∠BGD=∠C=60°
又四边形AEDF的对角互补,故∠GED=∠DFC
∴△DEG≌△DFC
故EG=CF
∴BE+CF=BE+EG=BG=![]() AB
AB
(3)取AB的中点G,连接DG
同(2),易证△DEG≌△DFC
故EG=CF
故BE-CF=BE-EG=BG=![]() AB
AB
设CN=x
在Rt△DCN中,CD=2x,DN=![]() x
x
在RT△DFN中,NF=DN=![]() x,故EG=CF=(
x,故EG=CF=(![]() -1)x
-1)x
BE=BG+EG=DC+CF=2x+(![]() -1)x=(
-1)x=(![]() +1)x
+1)x
故BE+CF=(![]() +1)x+(
+1)x+(![]() -1)x=2
-1)x=2![]() x
x
![]() (BE-CF)=
(BE-CF)=![]() [(
[(![]() +1)x-(
+1)x-(![]() -1)]=2
-1)]=2![]() x
x
故BE+CF=![]() (BE-CF)
(BE-CF)