题目内容
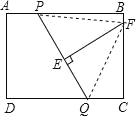
【题目】如图，在矩形ABCD中，AB=8，AD=6，P，Q分别是AB和CD上的任意一点，且AP=CQ，线段EF是PQ的垂直平分线，交BC于F，交PQ于E．设AP=x，BF=y，则y与x的函数关系式为______________．
【答案】y=
x﹣
．
【解析】
试题分析：连接PF，QF，∵线段EF是PQ的垂直平分线，∴PF=QF，∵在矩形ABCD中，AB=8，AD=6，∴BC=AD=6，∵AP=x，BF=y，∴PB=8﹣x，CF=6﹣y，∵CQ=AP=x，∴在Rt△PBF中，PF2=PB2+BF2=（8﹣x）2+y2，在Rt△CQF中，QF2=CF2+CQ2=（6﹣y）2+x2，∴（8﹣x）2+y2=（6﹣y）2+x2，即y=x﹣．故答案为：y=x﹣．
练习册系列答案
相关题目
【题目】某商店购进一种商品，每件商品进价30元．试销中发现这种商品每天的销售量y（件）与每件销售价x（元）的关系数据如下：
x | 30 | 32 | 34 | 36 |
y | 40 | 36 | 32 | 28 |
（1）已知y与x满足一次函数关系，根据上表，求出y与x之间的关系式（不写出自变量x的取值范围）；
（2）如果商店销售这种商品，每天要获得150元利润，那么每件商品的销售价应定为多少元？
（3）设该商店每天销售这种商品所获利润为w（元），求出w与x之间的关系式，并求出每件商品销售价定为多少元时利润最大？
