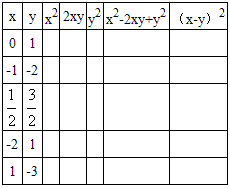题目内容
根据给出的x、y的值填表:| x | y | x2 | 2xy | y2 | x2-2xy+y2 | (x-y)2 | ||||
| 0 | 1 | |||||||||
| -1 | -2 | |||||||||
|
|
|||||||||
| -2 | 1 | |||||||||
| 1 | -3 |
当x=0,y=1时,x2-2xy+y2与(x-y)2的值相同吗?
当x=-1,y=-2时,x2-2xy+y2与(x-y)2的值相同吗?
是否当无论x、y是什么值,计算x2-2xy+y2与(x-y)2所得结果都相同吗?
由此你能推出x2-2xy+y2=(x-y)2吗?
总结:①给出代数式中字母的值,就能计算代数式的值,并且根据所给值的不同,求出的代数式的值也不同;②根据所给数值还可以发现一些规律.
分析:本题考查代数式的求值,对于不同的x、y,代入x2、2xy、y2、x2-2xy+y2、(x-y)2,然后比较x2-2xy+y2与(x-y)2的值.
解答:解:当x=0,y=1,
x2=0、2xy=0、y2=1、x2-2xy+y2=1、(x-y)2=1;
当x=-1,y=-2,
x2=1、2xy=4、y2=4、x2-2xy+y2=1、(x-y)2=1;
当x=
,y=
,
x2=
、2xy=
、y2=
、x2-2xy+y2=1、(x-y)2=1;
当x=-2,y=1,
x2=4、2xy=-4、y2=1、x2-2xy+y2=9、(x-y)2=9;
当x=1,y=-3,
x2=1、2xy=-6、y2=9、x2-2xy+y2=16、(x-y)2=16;
表格如图:
x2=0、2xy=0、y2=1、x2-2xy+y2=1、(x-y)2=1;
当x=-1,y=-2,
x2=1、2xy=4、y2=4、x2-2xy+y2=1、(x-y)2=1;
当x=
| 1 |
| 2 |
| 3 |
| 2 |
x2=
| 1 |
| 4 |
| 3 |
| 2 |
| 9 |
| 4 |
当x=-2,y=1,
x2=4、2xy=-4、y2=1、x2-2xy+y2=9、(x-y)2=9;
当x=1,y=-3,
x2=1、2xy=-6、y2=9、x2-2xy+y2=16、(x-y)2=16;
表格如图:
| x | y | x2 | 2xy | y2 | x2-2xy+y2 | (x-y)2 | ||||||||||
| 0 | 1 | 0 | 0 | 1 | 1 | 1 | ||||||||||
| -1 | -2 | 4 | 1 | 1 | ||||||||||||
|
|
|
|
|
1 | 1 | ||||||||||
| -2 | 1 | 4 | -4 | 1 | 9 | 9 | ||||||||||
| 1 | -3 | 1 | -6 | 9 | 16 | 16 |
点评:本题实际是验证:x2-2xy+y2=(x-y)2成立.

练习册系列答案
相关题目
根据给出的x、y的值填表.
| x | y | x2 | 2xy | y2 | x2-2xy+y 2 | (x-y)2 | ||||
| 0 | 1 | |||||||||
| -1 | -2 | |||||||||
|
|
|||||||||
| -2 | 1 | |||||||||
| 1 | -3 |