题目内容
若一个三角形的任意两条边都不相等,则称之为“不规则三角形”.顶点在一个正方体上的所有三角形中,这样的“不规则三角形”的个数为
- A.8
- B.18
- C.24
- D.36
C
分析:根据立方体的八个顶点之间线段长度仅有三种可能,分别得出所求的不规则三角形的个数.
解答: 解:不妨设立方体的边长为a,则在立方体的八个顶点之间线段长度仅有三种可能:
解:不妨设立方体的边长为a,则在立方体的八个顶点之间线段长度仅有三种可能:
边长为a,面对角线为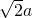 ,体对角线为
,体对角线为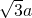 .立方体有四条体对角线,先考虑其中的一条如AC1,第三个顶点可以是B、C、D、A1、B1、D1中之一,
.立方体有四条体对角线,先考虑其中的一条如AC1,第三个顶点可以是B、C、D、A1、B1、D1中之一,
有6个不规则三角形.因此所求的不规则三角形的个数是6×4=24.
故选C.
点评:此题主要考查了勾股定理以及立体图形的性质,得出立方体的八个顶点之间线段长度仅有三种可能是解决问题的关键.
分析:根据立方体的八个顶点之间线段长度仅有三种可能,分别得出所求的不规则三角形的个数.
解答:
 解:不妨设立方体的边长为a,则在立方体的八个顶点之间线段长度仅有三种可能:
解:不妨设立方体的边长为a,则在立方体的八个顶点之间线段长度仅有三种可能:边长为a,面对角线为
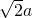 ,体对角线为
,体对角线为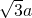 .立方体有四条体对角线,先考虑其中的一条如AC1,第三个顶点可以是B、C、D、A1、B1、D1中之一,
.立方体有四条体对角线,先考虑其中的一条如AC1,第三个顶点可以是B、C、D、A1、B1、D1中之一,有6个不规则三角形.因此所求的不规则三角形的个数是6×4=24.
故选C.
点评:此题主要考查了勾股定理以及立体图形的性质,得出立方体的八个顶点之间线段长度仅有三种可能是解决问题的关键.

练习册系列答案
相关题目