题目内容
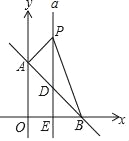
【题目】如图,平面直角坐标系中,直线AB:y=﹣x+b交y轴于点A,交x轴于点B,S△AOB=8.
(1)求点B的坐标和直线AB的函数表达式;
(2)直线a垂直平分OB交AB于点D,交x轴于点E,点P是直线a上一动点,且在点D的上方,设点P的纵坐标为m.
①用含m的代数式表示△ABP的面积;
②当S△ABP=6时,求点P的坐标;
③在②的条件下,在坐标轴上,是否存在一点Q,使得△ABQ与△ABP面积相等?若存在,直接写出点Q的坐标,若不存在,请说明理由.
【答案】(1)点B的坐标为(4,0),直线AB的函数表达式为y=﹣x+4;
(2)①S△ABP=2m﹣4;②点P的坐标为(2,5);③存在,点Q的坐标为(1,0)或(7,0)或(0,1)或(0,7).
【解析】
(1)利用一次函数图象上点的坐标特征可找出点A、B的坐标,结合S△AOB=8即可求出b值,进而可得出点B的坐标和直线AB的函数表达式;
(2)①由OB的长度结合直线a垂直平分OB,可得出OE、BE的长度,利用一次函数图象上点的坐标特征可求出点D的坐标,进而可用含m的代数式表示出DP的值,再利用三角形的面积公式即可用含m的代数式表示△ABP的面积;
②由①的结论结合S△ABP=6,即可求出m值,此题得解;
③分点Q在x轴及y轴两种情况考虑,利用三角形的面积公式即可求出点Q的坐标,此题得解.
解:(1)∵直线AB:y=﹣x+b交y轴于点A,交x轴于点B,
∴点A的坐标为(0,b),点B的坐标为(b,0).
∵S△AOB=![]() b2=8,
b2=8,
∴b=±4.
∵点A在y轴正半轴上,
∴b=4,
∴点B的坐标为(4,0),直线AB的函数表达式为y=﹣x+4;
(2)①∵直线a垂直平分OB,OB=4,
∴OE=BE=2,
当x=2时,y=﹣x+4=2,
∴点D的坐标为(2,2),
∵点P的坐标为(2,m)(m>2),
∴PD=m﹣2,
∴S△ABP=S△APD+S△BPD,
=![]() DPOE+
DPOE+![]() DPBE,
DPBE,
=![]() ×2(m﹣2)+
×2(m﹣2)+![]() ×2(m﹣2)=2m﹣4;
×2(m﹣2)=2m﹣4;
②∵S△ABP=6,
∴2m﹣4=6,
∴m=5,
∴点P的坐标为(2,5);
③假设存在.
当点Q在x轴上时,设其坐标为(x,0),
∵S△ABQ=![]() AOBQ=
AOBQ=![]() ×4×|x﹣4|=6,
×4×|x﹣4|=6,
∴x1=1,x2=7,
∴点Q的坐标为(1,0)或(7,0);
当点Q在y轴上时,设其坐标为(0,y),
∵S△ABQ=![]() BOAQ=
BOAQ=![]() ×4×|y﹣4|=6,
×4×|y﹣4|=6,
∴y1=1,y2=7,
∴点Q的坐标为(0,1)或(0,7).
综上所述:假设成立,即在坐标轴上,存在一点Q,使得△ABQ与△ABP面积相等,且点Q的坐标为(1,0)或(7,0)或(0,1)或(0,7).

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案