题目内容
【题目】已知,在矩形ABCD中,AB=a,BC=b,动点M从点A出发沿边AD向点D运动(点M与点A、点D不重合).
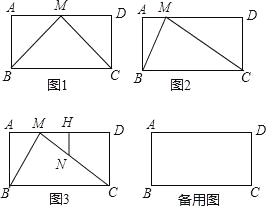
(1)如图1,当b=2a,点M运动到边AD的中点时,请证明∠BMC=90°;
(2)如图2,当a=2,b=5,求点M运动到什么位置时,∠BMC=90°;
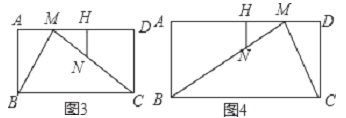
(3)如图3,在第(2)问的条件下,若另一动点N从点C出发沿边C→M→B运动,且点M、点N的出发时间与运动速度都相同,过点N作AD和垂线交AD于点H,当△MNH与△MBC相似时,求MH的长.
【答案】(1)详见解析;(2)AM=1或4时,∠BMC=90°;(3)△MNH与△MBC相似时,MH=8﹣![]() 或
或![]() ﹣2.
﹣2.
【解析】
试题分析:(1)由b=2a,点M是AD的中点,可得AB=AM=MD=DC=a,又由四边形ABCD是矩形,即可求得∠AMB=∠DMC=45°,则可求得∠BMC=90°;(2)根据已知条件得到∠AMB+∠DMC=90°,根据余角的性质得到∠ABM=∠DMC,根据相似三角形的性质得到![]() ,代入数据即可得到结论.(3)①当点N在CM上时,由△MNH与△MBC相似,得到∠BMC=∠MHN=90°,当AM=CN=1时,根据相似三角形的性质列方程求得结论;当AM=CN=4时,DM=1,CM=
,代入数据即可得到结论.(3)①当点N在CM上时,由△MNH与△MBC相似,得到∠BMC=∠MHN=90°,当AM=CN=1时,根据相似三角形的性质列方程求得结论;当AM=CN=4时,DM=1,CM=![]() <4,这种情况不存在;②当点N在BM上时,当AM=CN=1时,同理这种情况不存在;当AM=CN=4时,即CM+MN=4,根据相似三角形的性质即可得到结论.
<4,这种情况不存在;②当点N在BM上时,当AM=CN=1时,同理这种情况不存在;当AM=CN=4时,即CM+MN=4,根据相似三角形的性质即可得到结论.
试题解析:(1)证明:∵b=2a,点M是AD的中点,
∴AB=AM=MD=DC=a,
又∵在矩形ABCD中,∠A=∠D=90°,
∴∠AMB=∠DMC=45°,
∴∠BMC=90°.
(2)解:若∠BMC=90°,
则∠AMB+∠DMC=90°,
又∵∠AMB+∠ABM=90°,
∴∠ABM=∠DMC,
又∵∠A=∠D=90°,
∴△ABM∽△DMC,
∴![]() ,
,
设AM=x,则![]() ,
,
∴x=1或4,
∴AM=1或4时,∠BMC=90°;
(3)解:①当点N在CM上时,
∵△MNH与△MBC相似,
∴∠BMC=∠MHN=90°,
当AM=CN=1时,
∴DM=4,∴CM=2![]() ,
,
∴MN=2![]() ﹣1,
﹣1,
∵NH⊥AD,∠D=90°,
∴NH∥CD,
∴![]() ,
,
∴![]() ,
,
∴MH=8﹣![]() ;
;
当AM=CN=4时,
DM=1,CM=![]() <4,
<4,
∴这种情况不存在;
②当点N在BM上时,
当AM=CN=1时,同理这种情况不存在;
当AM=CN=4时,即CM+MN=4,
∵CM=![]() ,
,
∴MN=4﹣![]() ,BM=2
,BM=2![]() ,
,
∵HN∥AB,
∴△MHN∽ABM,
∴![]() ,即
,即![]() ,
,
∴MH=![]() ﹣2.
﹣2.
综上所述:△MNH与△MBC相似时,MH=8﹣![]() 或
或![]() ﹣2.
﹣2.

 阅读快车系列答案
阅读快车系列答案