题目内容
证明题
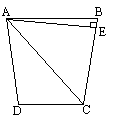
如图，已知△ABC中，AB＝AC，∠A＝
，D是BC的中点，E、F分别是AB、AC上的动点且满足ED⊥DF．是否存在AE＝AF的情形？并给予证明．
答案：
解析：
解析：
|
当∠BDE＝∠FDC＝ |
时，AE＝AF．因为在△BDE和△CDF中，∠B＝∠C＝
，∠EDB＝∠FDC＝
，BD＝DC，所以△BED≌△CFD，所以BE＝CF．又AB＝AC，所以AE＝AF
练习册系列答案
相关题目
，AB＝AC，BD⊥AE于D，CE⊥AE于E，求证：BD＝DE＋CE．
