题目内容
如图①:已知点C为线段AB上一点,且D、E分别是线段AB、BC的中点,
(1)若AC=5cm,BC=4cm,试求线段DE的长度.
(2)如果(1)中的BC=a,其他条件不变,试求DE的长度.
(3)根据(1)(2)的计算结果,有关线段DE的长度你能得出什么结论?
(4)如图②,已知∠AOC=α,∠BOC=β,且OD、OE分别为∠AOB、∠BOC的角平分线,请直接写出∠DOE度数的表达式.

(1)若AC=5cm,BC=4cm,试求线段DE的长度.
(2)如果(1)中的BC=a,其他条件不变,试求DE的长度.
(3)根据(1)(2)的计算结果,有关线段DE的长度你能得出什么结论?
(4)如图②,已知∠AOC=α,∠BOC=β,且OD、OE分别为∠AOB、∠BOC的角平分线,请直接写出∠DOE度数的表达式.

分析:(1)由AC+BC求出AB的长,再由D、E分别为AB、BC的中点,根据线段中点定义求出DB与BE的长,由DB-BE即可求出DE的长;
(2)同理即可求出DE的长;
(3)根据(1)和(2)归纳总结即可得到结果;
(4)由∠AOC+∠COB求出∠AOB的度数,再由OD为∠AOC的平分线,OE为∠COB的平分线,求出∠DOB与∠COE的度数,由∠BOD-BOE即可表示出∠DOE.
(2)同理即可求出DE的长;
(3)根据(1)和(2)归纳总结即可得到结果;
(4)由∠AOC+∠COB求出∠AOB的度数,再由OD为∠AOC的平分线,OE为∠COB的平分线,求出∠DOB与∠COE的度数,由∠BOD-BOE即可表示出∠DOE.
解答:解:(1)∵AC=5cm,BC=4cm,
∴AB=AC+BC=9cm,
∵D、E分别是AB、BC的中点,
∴DB=
AB=4.5cm,BE=
BC=2cm,
∴DE=DB-BE=2.5cm;
(2)∵AC=5,BC=a,
∴AB=AC+BC=5+a,
∵D、E分别是AB、BC的中点,
∴DB=
AB=
(5+a),BE=
BC=
a,
∴DE=DB-BE=2.5;
(3)结论:DE的长只与AC的长有关,且DE=
AC;
(4)∠DOE=
∠AOC=
α,理由为:
证明:∵∠AOC=α,∠BOC=β,
∴∠AOB=∠AOC+∠BOC=α+β,
∵OD、OE分别为∠AOB、∠BOC的角平分线,
∴∠BOD=
∠AOB=
(α+β),∠COE=
∠BOC=
β,
则∠DOE=∠BOD-∠COE=
α.
∴AB=AC+BC=9cm,
∵D、E分别是AB、BC的中点,
∴DB=
| 1 |
| 2 |
| 1 |
| 2 |
∴DE=DB-BE=2.5cm;
(2)∵AC=5,BC=a,
∴AB=AC+BC=5+a,
∵D、E分别是AB、BC的中点,
∴DB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴DE=DB-BE=2.5;
(3)结论:DE的长只与AC的长有关,且DE=
| 1 |
| 2 |
(4)∠DOE=
| 1 |
| 2 |
| 1 |
| 2 |
证明:∵∠AOC=α,∠BOC=β,
∴∠AOB=∠AOC+∠BOC=α+β,
∵OD、OE分别为∠AOB、∠BOC的角平分线,
∴∠BOD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
则∠DOE=∠BOD-∠COE=
| 1 |
| 2 |
点评:此题考查了角的计算,以及角平分线定义,弄清题中的规律是解本题的关键.

练习册系列答案
相关题目


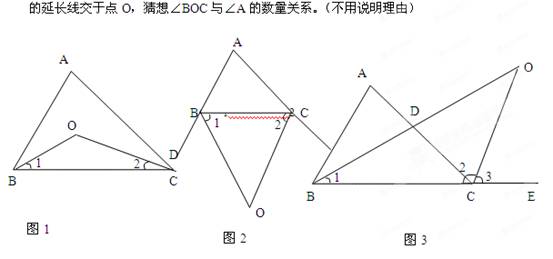 (3)如图3,已知:BD为△ABC的角平分线,CO为△ABC的外角平分线,OB
(3)如图3,已知:BD为△ABC的角平分线,CO为△ABC的外角平分线,OB