题目内容
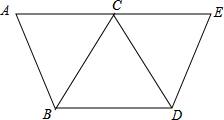 如图,已知点C为线段AE的中点,∠A=∠E,∠ACB=∠ECD.
如图,已知点C为线段AE的中点,∠A=∠E,∠ACB=∠ECD.(1)求证:△ACB≌△ECD;
(2)求证:∠CBD=∠CDB.
分析:(1)由点C为线段AE的中点就可以得出AC=AE,再由条件就可以得出△ACB≌△ECD;
(2)由△ACB≌△ECD就可以得出BC=CD,由等边对等角就可以得出结论.
(2)由△ACB≌△ECD就可以得出BC=CD,由等边对等角就可以得出结论.
解答:解:(1)∵点C为线段AE的中点,
∴CA=CE
在△ACB和△ECD中,
,
∴△ACB≌△ECD(ASA);
(2)∵△ACB≌△ECD,
∴CB=CD,
∴∠CBD=∠CDB.
∴CA=CE
在△ACB和△ECD中,
|
∴△ACB≌△ECD(ASA);
(2)∵△ACB≌△ECD,
∴CB=CD,
∴∠CBD=∠CDB.
点评:本题考查了线段中点的性质的运用,三角形全等的判定与性质的运用,等腰三角形的判定的运用,解答时证明三角形全等是关键.

练习册系列答案
相关题目
 如图,已知点C为线段AE上一点,AE=8cm,△ABC和△CDE为AE同侧的两个等边三角形,连接BE交CD于N,连接AD交BC于M,连接MN.
如图,已知点C为线段AE上一点,AE=8cm,△ABC和△CDE为AE同侧的两个等边三角形,连接BE交CD于N,连接AD交BC于M,连接MN.
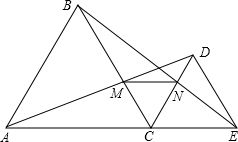 如图,已知点C为线段AE上一点,AE=8cm,△ABC和△CDE为AE同侧的两个等边三角形,连接BE交CD于N,连接AD交BC于M,连接MN.
如图,已知点C为线段AE上一点,AE=8cm,△ABC和△CDE为AE同侧的两个等边三角形,连接BE交CD于N,连接AD交BC于M,连接MN.