МвДҝДЪИЭ
ЎҫМвДҝЎҝЈЁ1Ј©ЈЁФД¶БУлЦӨГчЈ©
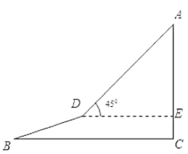
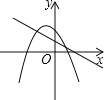
ИзНј1Ј¬ФЪХэ![]() өДНвҪЗ
өДНвҪЗ![]() ДЪТэЙдПЯ
ДЪТэЙдПЯ![]() Ј¬ЧчөгC№ШУЪ
Ј¬ЧчөгC№ШУЪ![]() өД¶ФіЖөгEЈЁөгEФЪ
өД¶ФіЖөгEЈЁөгEФЪ![]() ДЪЈ©Ј¬Б¬ҪУ
ДЪЈ©Ј¬Б¬ҪУ![]() Ј¬
Ј¬![]() Ўў
Ўў![]() ·ЦұрҪ»
·ЦұрҪ»![]() УЪөгFЎўGЈ®
УЪөгFЎўGЈ®
ўЩНкіЙЦӨГчЈә![]() өгEКЗөгC№ШУЪ
өгEКЗөгC№ШУЪ![]() өД¶ФіЖөгЈ¬
өД¶ФіЖөгЈ¬
![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј®
Ј®
![]() Хэ
Хэ![]() ЦРЈ¬
ЦРЈ¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬
![]() Ј¬өГ
Ј¬өГ![]() Ј®
Ј®
ФЪ![]() ЦРЈ¬
ЦРЈ¬![]() Ј¬
Ј¬![]() ______
______![]() Ј®
Ј®
ФЪ![]() ЦРЈ¬
ЦРЈ¬![]() Ј¬
Ј¬![]() ______
______![]() Ј®
Ј®
ўЪЗуЦӨЈә![]() Ј®
Ј®
ЈЁ2Ј©ЈЁАаұИУлМҪҫҝЈ©
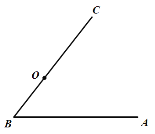
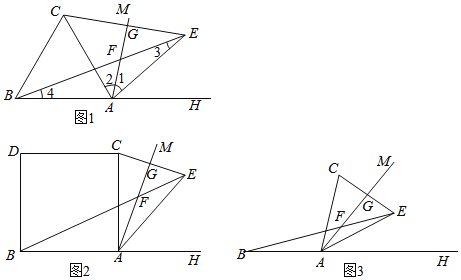
°СЈЁ1Ј©ЦРөДЎ°Хэ![]() ЎұёДОӘЎ°Хэ·ҪРО
ЎұёДОӘЎ°Хэ·ҪРО![]() ЎұЈ¬ЖдУаМхјюІ»ұдЈ¬ИзНј2Ј®АаұИМҪҫҝЈ¬ҝЙөГЈә
ЎұЈ¬ЖдУаМхјюІ»ұдЈ¬ИзНј2Ј®АаұИМҪҫҝЈ¬ҝЙөГЈә
ўЩ![]() ______
______![]() Ј»
Ј»
ўЪПЯ¶О![]() Ўў
Ўў![]() Ўў
Ўў![]() Ц®јдҙжФЪКэБҝ№ШПө___________Ј®
Ц®јдҙжФЪКэБҝ№ШПө___________Ј®
ЈЁ3Ј©ЈЁ№йДЙУлНШХ№Ј©
ИзНј3Ј¬өгAФЪЙдПЯ![]() ЙПЈ¬
ЙПЈ¬![]() Ј¬
Ј¬![]() Ј¬ФЪ
Ј¬ФЪ![]() ДЪТэЙдПЯ
ДЪТэЙдПЯ![]() Ј¬ЧчөгC№ШУЪ
Ј¬ЧчөгC№ШУЪ![]() өД¶ФіЖөгEЈЁөгEФЪ
өД¶ФіЖөгEЈЁөгEФЪ![]() ДЪЈ©Ј¬Б¬ҪУ
ДЪЈ©Ј¬Б¬ҪУ![]() Ј¬
Ј¬![]() Ўў
Ўў![]() ·ЦұрҪ»
·ЦұрҪ»![]() УЪөгFЎўGЈ®ФтПЯ¶О
УЪөгFЎўGЈ®ФтПЯ¶О![]() Ўў
Ўў![]() Ўў
Ўў![]() Ц®јдөДКэБҝ№ШПөОӘ__________Ј®
Ц®јдөДКэБҝ№ШПөОӘ__________Ј®
Ўҫҙр°ёЎҝЈЁ1Ј©ўЩ60ЎгЈ¬30ЎгЈ»ўЪЦӨГчјыҪвОцЈ»ЈЁ2Ј©ўЩ45ЎгЈ»ўЪBF=![]() (AF+FG)Ј»ЈЁ3Ј©
(AF+FG)Ј»ЈЁ3Ј©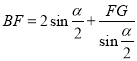 Ј®
Ј®
ЎҫҪвОцЎҝ
ЈЁ1Ј©ўЩёщҫЭөИБҝҙъ»»әНЦұҪЗИэҪЗРОөДРФЦКјҙҝЙИ·¶Ёҙр°ёЈ»ўЪФЪFBЙПИЎAN=AFЈ¬Б¬ҪУANЈ®ПИЦӨГчЎчAFNКЗөИұЯИэҪЗРОЈ¬өГөҪ ЎПBAN=ЎП2=ЎП1Ј¬И»әуФЩЦӨГчЎчABNЎХЎчAEFЈ¬И»әуАыУГИ«өИИэҪЗРОөДРФЦКТФј°ПЯ¶ОөДәНІојҙҝЙЦӨГчЈ»
ЈЁ2Ј©АаұИЈЁ1Ј©өД·Ҫ·ЁјҙҝЙЧчҙрЈ»
ЈЁ3Ј©ёщҫЭЈЁ1Ј©ЈЁ2Ј©өДҪбВЫЈ¬јҙҝЙЧЬҪбіцҙр°ёЈ®
ҪвЈәЈЁ1Ј©ўЩЎЯ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]()
Ўа![]() Ј¬јҙ
Ј¬јҙ![]() 60ЎгЈ»
60ЎгЈ»
ЎЯ![]()
Ўа![]()
№Кҙр°ёОӘ60ЎгЈ¬30ЎгЈ»
ўЪФЪFBЙПИЎFN=AFЈ¬Б¬ҪУAN
ЎЯЎПAFN=ЎПEFG=60Ўг
ЎаЎчAFNКЗөИұЯИэҪЗРО
ЎаAF=FN=AN
ЎЯFN=AF
ЎаЎПBAC=ЎПNAF=60Ўг
ЎаЎПBAN+ЎПNAC=ЎПNAC+ЎП2
ЎаЎПBAN=ЎП2
ЎЯөгC№ШУЪ![]() өД¶ФіЖөгE
өД¶ФіЖөгE
ЎаЎП2=ЎП1,AC=AE
ЎаЎПBAN=ЎП2=ЎП1
ЎЯAB=AC
ЎаAB=AE
ФЪЎчABNәНЎчAEF
FN=AF,ЎПBAN=ЎП1,AB=AE
ЎаЎчABNЎХЎчAEF
ЎаBN=EF
ЎЯAGЎНCEЈ¬ЎПFEG=30Ўг
ЎаEF=2FG
ЎаBN=EF=2FG
ЎЯBF=BN+NF
ЎаBF=2FG+AF
ЈЁ2Ј©ўЩ![]() өгEКЗөгC№ШУЪ
өгEКЗөгC№ШУЪ![]() өД¶ФіЖөгЈ¬
өД¶ФіЖөгЈ¬
![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј®
Ј®
![]() Хэ·ҪРОABCDЦРЈ¬
Хэ·ҪРОABCDЦРЈ¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬
![]() Ј¬өГ
Ј¬өГ![]() Ј®
Ј®
ФЪ![]() ЦРЈ¬
ЦРЈ¬![]() Ј¬
Ј¬
![]() 45
45![]() Ј®
Ј®
ФЪ![]() ЦРЈ¬
ЦРЈ¬![]() Ј¬
Ј¬
![]() 45
45![]() Ј®
Ј®
№Кҙр°ёОӘ45ЎгЈ»
ўЪФЪFBЙПИЎFN=AFЈ¬Б¬ҪУAN
ЎЯЎПAFN=ЎПEFG=45Ўг
ЎаЎчAFNКЗөИСьЦұҪЗИэҪЗРО
ЎаЎПNAF=90ЎгЈ¬AF=AN
ЎаЎПBAN+ЎПNAC=ЎПNAC+ЎП2=90Ўг,FN=![]() AF
AF
ЎаЎПBAN=ЎП2
ЎЯөгC№ШУЪ![]() өД¶ФіЖөгE
өД¶ФіЖөгE
ЎаЎП2=ЎП1,AC=AE
ЎаЎПBAN=ЎП2=ЎП1
ЎЯAB=AC
ЎаAB=AE
ФЪЎчABNәНЎчAEF
FN=AF,ЎПBAN=ЎП1,AB=AE
ЎаЎчABNЎХЎчAEF
ЎаBN=EF
ЎЯAGЎНCEЈ¬ЎПFEG=45Ўг
ЎаEF=![]() FG
FG
ЎаBN=EF=![]() FG
FG
ЎЯBF=BN+NF
ЎаBF=![]() FG+
FG+![]() AF
AF
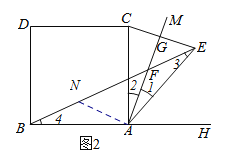
ЈЁ3Ј©УЙЈЁ1Ј©өГЈәөұЎПBAC=60ЎгКұ
BF=AF+2FG=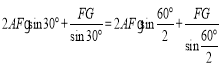
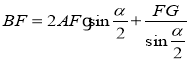 Ј»
Ј»
УЙЈЁ2Ј©өГЈәөұЎПBAC=90ЎгКұ
BF=![]() AF+
AF+![]() 2FG=
2FG=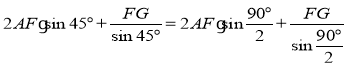 Ј»
Ј»
ТФҙЛАаНЖЈ¬өұөұЎПBAC=![]() 60ЎгКұЈ¬
60ЎгКұЈ¬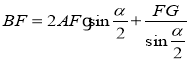 Ј®
Ј®

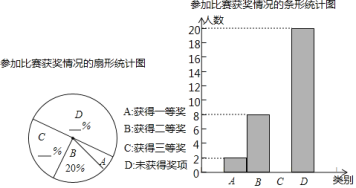
ЎҫМвДҝЎҝОӘБЛҪвС§ЙъХЖОХА¬»ш·ЦАаЦӘК¶өДЗйҝцЈ¬ФцЗҝС§Йъ»·ұЈТвК¶Ј¬ДіС§РЈҫЩРРБЛЎ°А¬»ш·ЦАаИЛИЛУРФрЎұөДЦӘК¶ІвКФ»о¶ҜЈ¬ПЦҙУёГРЈЖЯЎў°ЛДкј¶ЦРёчЛж»ъійИЎ20ГыС§ЙъөДІвКФіЙјЁЈЁВъ·Ц10·ЦЈ¬6·Цј°6·ЦТФЙПОӘәПёсЈ©ҪшРРХыАнЎўГиКцәН·ЦОцЈ¬ПВГжёшіцБЛІҝ·ЦРЕПўЈ®
ЖЯДкј¶20ГыС§ЙъөДІвКФіЙјЁОӘЈә
7Ј¬8Ј¬7Ј¬9Ј¬7Ј¬6Ј¬5Ј¬9Ј¬10Ј¬9Ј¬8Ј¬5Ј¬8Ј¬7Ј¬6Ј¬7Ј¬9Ј¬7Ј¬10Ј¬6Ј®
ЖЯЎў°ЛДкј¶ійИЎөДС§ЙъөДІвКФіЙјЁөДЖҪҫщКэЎўЦЪКэЎўЦРО»КэЎў8·Цј°ТФЙПИЛКэЛщХј°Щ·ЦұИИзПВұнЛщКҫЈә
Дкј¶ | ЖҪҫщКэ | ЦЪКэ | ЦРО»Кэ | 8·Цј°ТФЙПИЛКэЛщХј°Щ·ЦұИ |
ЖЯДкј¶ | 7.5 | a | 7 | 45% |
°ЛДкј¶ | 7.5 | 8 | b | c |
°ЛДкј¶20ГыС§ЙъөДІвКФіЙјЁМхРОНіјЖНјИзНјЈә
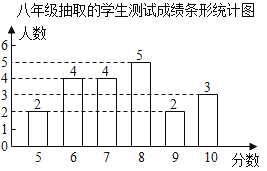
ёщҫЭТФЙПРЕПўЈ¬ҪвҙрПВБРОКМвЈә
ЈЁ1Ј©ЦұҪУРҙіцЙПКцұнЦРөДaЈ¬bЈ¬cөДЦөЈ»
ЈЁ2Ј©ёщҫЭТФЙПКэҫЭЈ¬ДгИПОӘёГРЈЖЯЎў°ЛДкј¶ЦРДДёцДкј¶С§ЙъХЖОХА¬»ш·ЦАаЦӘК¶ҪПәГЈҝЗлЛөГчАнУЙЈЁРҙіцТ»МхАнУЙјҙҝЙЈ©Ј»
ЈЁ3Ј©ёГРЈЖЯЎў°ЛДкј¶№І1200ГыС§ЙъІОјУБЛҙЛҙОІвКФ»о¶ҜЈ¬№АјЖІОјУҙЛҙОІвКФ»о¶ҜіЙјЁәПёсөДС§ЙъИЛКэКЗ¶аЙЩЈҝ