��Ŀ����
����Ŀ����ƽ��ֱ������ϵxOy�У�����P�͵�P1����y��Գƣ���P1�͵�P2����ֱ��l�Գƣ���Ƶ�P2�ǵ�P����y�ᣬֱ��l�Ķ��ζԳƵ㣮
��1����ͼ1����A����1��0���� 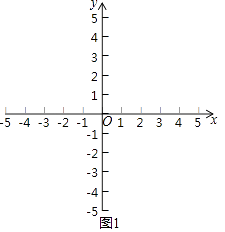
������B�ǵ�A����y�ᣬֱ��l1��x=2�Ķ��ζԳƵ㣬���B������Ϊ��
������C����5��0���ǵ�A����y�ᣬֱ��l2��x=a�Ķ��ζԳƵ㣬��a��ֵΪ��
������D��2��1���ǵ�A����y�ᣬֱ��l3�Ķ��ζԳƵ㣬��ֱ��l3�ı���ʽΪ��
��2����ͼ2����O�İ뾶Ϊ1������O�ϴ��ڵ�M��ʹ�õ�M'�ǵ�M����y�ᣬֱ��l4��x=b�Ķ��ζԳƵ㣬�ҵ�M'������y= ![]() x��x��0���ϣ�b��ȡֵ��Χ����
x��x��0���ϣ�b��ȡֵ��Χ���� 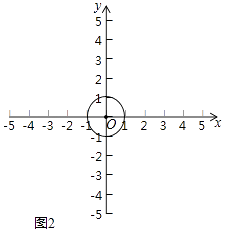
��3��E��t��0����x���ϵĶ��㣬��E�İ뾶Ϊ2������E�ϴ��ڵ�N��ʹ�õ�N'�ǵ�N����y�ᣬֱ��l5��y= ![]() x+1�Ķ��ζԳƵ㣬�ҵ�N'��y���ϣ���t��ȡֵ��Χ��
x+1�Ķ��ζԳƵ㣬�ҵ�N'��y���ϣ���t��ȡֵ��Χ��
���𰸡�
��1����3.0����-2��y=��x+2
��2���� ![]() ��b��1
��b��1
��3����ͼ6�У����E����y��ĶԳƵ�ΪE1��E1����ֱ��y= ![]() x+1�ĶԳƵ�ΪE�䣬��֪����N�ڡ�E���˶�ʱ����N���ڡ�E�����˶����ɴ˿ɼ�����E����y�����л��ཻʱ����������
x+1�ĶԳƵ�ΪE�䣬��֪����N�ڡ�E���˶�ʱ����N���ڡ�E�����˶����ɴ˿ɼ�����E����y�����л��ཻʱ����������
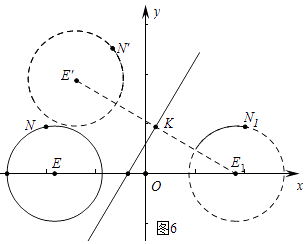
����E1E�佻ֱ��y= ![]() x+1��K����ֱ֪��E1E��Ľ���ʽΪy=��
x+1��K����ֱ֪��E1E��Ľ���ʽΪy=�� ![]() x��
x�� ![]() t��
t��
��  ���
��� 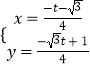 ��
��
��K�� ![]() ��
�� ![]() ����
����
��KE1=KE�䣬
��E�䣨 ![]() ��
�� ![]() ����
����
����E����y������ʱ��| ![]() |=2�����t=
|=2�����t= ![]() ��4��
��4�� ![]() +4��
+4��
��������������������t��ȡֵ��ΧΪ ![]() ��4��t��
��4��t�� ![]() +4
+4
���������⣺��1.������ͼ1�У���A����1��0������y��ĶԳƵ�A1��1��0����A1����ֱ��x=2�ĶԳƵ�B��3��0���� 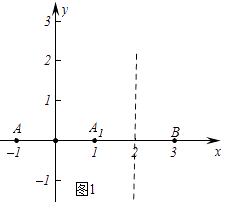
����ͼ2�У�������C����5��0����A1��1��0������A1��C����ֱ��x=a�Գƣ�
��a=��2��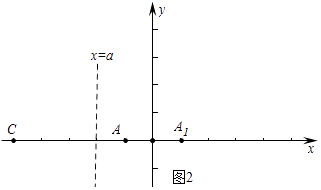
����ͼ3�У���A1��1��0����D��2��1����
��ֱ��A1D�Ľ���ʽΪy=x��1���߶�A1D���д��ߵĽ���ʽΪy=��x+2��
��ֱ��l3�Ľ���ʽΪy=��x+2��
�ʴ𰸷ֱ�Ϊ��3��0����a=��2��y=��x+2��
��2.����ͼ4�У�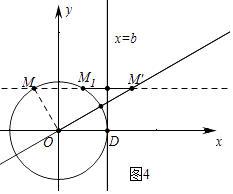
������b= ![]() MM�䣬�ɴ˿�֪����MM���ֵ���ʱ���ɵ�b�����ֵ��
MM�䣬�ɴ˿�֪����MM���ֵ���ʱ���ɵ�b�����ֵ��
��ֱ��OM��Ľ���ʽΪy= ![]() x��
x��
���MM��O=��M��OD=30�㣬
��OM=1����֪��OM��OM��ʱ��MM���ֵ������ֵΪ2��
��b�����ֵΪ1��
��ͼ5�У���֪����M��x�����������ʱ���ɵ�b����Сֵ����СֵΪ�� ![]() ��
��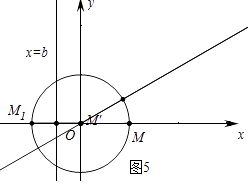
��������������������bȡֵ��ΧΪ�� ![]() ��b��1��
��b��1��
���Դ��ǩ� ![]() ��b��1��
��b��1��

 ���㼤�������100�ִ��Ծ�ϵ�д�
���㼤�������100�ִ��Ծ�ϵ�д�