题目内容
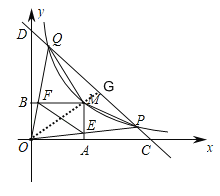
【题目】如图1,在平面直角坐标系中,反比例函数y=![]() (m为常数,m>2,x>0)的图象过点P(m,2)和Q(2,m),直线PQ与x轴,y轴分别交于C,D两点,点M(x,y)是反比例函数图象上的一个动点,过点M分别作x轴和y轴的垂线,垂足分别为A,B.MA交OP于点E,MB交OQ于点F,连接EF,MP,MQ
(m为常数,m>2,x>0)的图象过点P(m,2)和Q(2,m),直线PQ与x轴,y轴分别交于C,D两点,点M(x,y)是反比例函数图象上的一个动点,过点M分别作x轴和y轴的垂线,垂足分别为A,B.MA交OP于点E,MB交OQ于点F,连接EF,MP,MQ
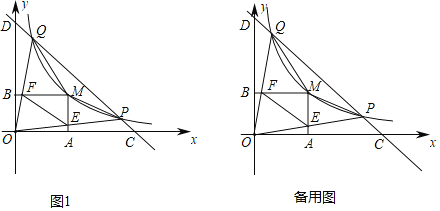
(1)当m=4时,求线段CD的长;
(2)当2<x<m时,若仅存在唯一的点M使得△MPQ的面积等于m﹣2,求此时点M的坐标;
(3)当2<x<m时,记以线段OE,OF为两直角边的三角形外接圆面积为S1;记三角形△MEF的外接圆面积为S2;记以PC为直径的圆面积为S3;记以QD为直径的圆面积为S4;试比较S1,S2+S3+S4的大小.
【答案】(1) 6![]() ;(2) M(4,4);(3) S1=S2+S3+S4,理由见解析
;(2) M(4,4);(3) S1=S2+S3+S4,理由见解析
【解析】
(1)求出直线PQ的解析式,再求出点C,D的坐标即可解决问题.
(2)由题意当2<x<m时,若仅存在唯一的点M使得△MPQ的面积等于m﹣2,根据反比例函数是关于直线y=x对称的,可知点M在直线y=x上,可得M(![]() ,
,![]() ),然后求出直线PQ的解析式,连接OM交CD于G,求出OG,OM,可得MG的长,然后结合P,Q坐标,可得PQ的长,再利用三角形的面积公式构建方程即可解决问题;
),然后求出直线PQ的解析式,连接OM交CD于G,求出OG,OM,可得MG的长,然后结合P,Q坐标,可得PQ的长,再利用三角形的面积公式构建方程即可解决问题;
(3)设M(a,![]() ),由(2)可知D(0,2+m),C(2+m,0),可得DQ=
),由(2)可知D(0,2+m),C(2+m,0),可得DQ=![]() ,PC=
,PC=![]() ,然后易得直线OP的解析式为y=
,然后易得直线OP的解析式为y=![]() ,直线OQ的解析式为y=
,直线OQ的解析式为y=![]() ,求出E(a,
,求出E(a,![]() ),F(
),F(![]() ,
,![]() ),再根据直角三角形外接圆的性质和圆的周长公式求出S1,S2,S3,S4,即可判断.
),再根据直角三角形外接圆的性质和圆的周长公式求出S1,S2,S3,S4,即可判断.
解:(1)当m=4时,Q(2,4),P(4,2),
设直线PQ的解析式为y=kx+b(k≠0),
则![]() ,解得:
,解得:![]() ,
,
∴直线PQ的解析式为y=﹣x+6,
令y=0则x=6,令x=0则y=6,
∴C(6,0),D(0,6),
∴OC=OD=6,
∵∠COD=90°,
∴CD=![]() ;
;
(2)∵当2<x<m时,若仅存在唯一的点M使得△MPQ的面积等于m﹣2,
∴根据反比例函数关于直线y=x对称,可知点M在直线y=x上,
∴M(![]() ,
,![]() ),
),
∴OM=![]() ,
,
设直线PQ的解析式为y=kx+b(k≠0),
则![]() ,解得:
,解得:![]() ,
,
∴直线PQ的解析式为y=﹣x+2+m,
令x=0则y=2+m,令y=0则x=2+m,
∴D(0,2+m),C(2+m,0),
∴CD=![]() ,
,
连接OM交CD于G,
∵△COD是等腰直角三角形,点M在直线y=x上,
∴OG⊥CD,
∴OG=![]() ,
,
∴MG=![]() ,
,
∵P(m,2),Q(2,m),
∴PQ=![]() ,
,
由题意得: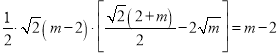 ,
,
解得m=8或0(舍去),
∴M(4,4);
(3)设M(a,![]() ),
),
由(2)可得D(0,2+m),C(2+m,0)
∴DQ=![]() ,PC=
,PC=![]() ,
,
易得直线OP的解析式为y=![]() ,直线OQ的解析式为y=
,直线OQ的解析式为y=![]() ,
,
∴E(a,![]() ),F(
),F(![]() ,
,![]() ),
),
∴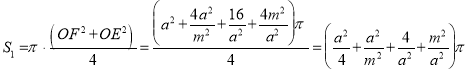
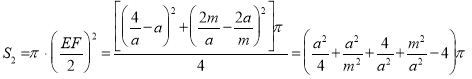 ,
,
S3=S4=2π,
∴S2+S3+S4=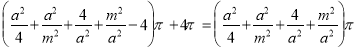 =S1,
=S1,
∴S1=S2+S3+S4.