题目内容
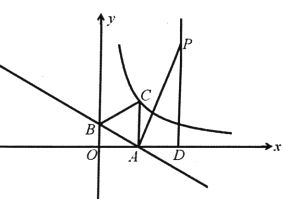
【题目】如图,已知B′C′∥BC,C′D′∥CD,D′E′∥DE.
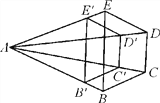
(1)求证:四边形BCDE位似于四边形B′C′D′E′;
(2)若![]() =3,S四边形BCDE=20,求S四边形B′C′D′E′.
=3,S四边形BCDE=20,求S四边形B′C′D′E′.
【答案】(1)见解析;(2)![]()
【解析】试题分析:
(1)由已知条件易得: ![]() ,结合四边形B′C′D′E′和BCDE中对应顶点的连线相交于点A,即可得到两个四边形是位似图形的结论;
,结合四边形B′C′D′E′和BCDE中对应顶点的连线相交于点A,即可得到两个四边形是位似图形的结论;
(2)由![]() 可得
可得![]() ,结合四边形B′C′D′E′和BCDE是位似图形即可得到:四边形B′C′D′E′和BCDE的相似比为
,结合四边形B′C′D′E′和BCDE是位似图形即可得到:四边形B′C′D′E′和BCDE的相似比为![]() ,结合S四边形BCDE=20,即可求得S四边形B′C′D′E′=
,结合S四边形BCDE=20,即可求得S四边形B′C′D′E′=![]() .
.
试题解析:
(1)∵B′C′∥BC,C′D′∥CD,D′E′∥DE,
∴![]() ,
,
又∵四边形B′C′D′E′和BCDE中对应顶点的连线相交于点A,
∴四边形B′C′D′E′和BCDE是位似图形;
(2)∵![]() ,
,
∴![]() ,
,
又∵四边形B′C′D′E′和BCDE是位似图形,
∴四边形B′C′D′E′和BCDE的相似比为![]() ,
,
∴S四边形B′C′D′E′:S四边形BCDE=9:16,
又∵S四边形BCDE=20,
∴S四边形B′C′D′E′=![]() .
.

练习册系列答案
相关题目