题目内容
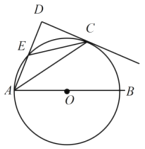
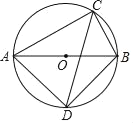
【题目】如图,△ABC内接于⊙O,AB是⊙O直径,∠ACB的平分线交⊙O于D,若AC=m,BC=n,则CD的长为_____(用含m、n的代数式表示).
【答案】![]()
【解析】
如图,作DE⊥CA于E,DF⊥BC交CB延长线于F,可得DE=DF,四边形DECF是正方形,利用HL可证Rt△ADE≌Rt△BDF,则AE=BF,进一步即得CE+CF=AC+BC,进而可得CE的长,然后利用等腰直角三角形的性质即可求出CD的长.
解:如图,作DE⊥CA于E,DF⊥BC交CB延长线于F,则∠CED=∠CFD=90°,

∵AB是直径,
∴∠ECF=90°,
∴四边形DECF是矩形,
∵DC平分∠ACB,DE⊥CA,DF⊥CB,
∴DE=DF,
∴四边形DECF是正方形,
∵∠DCA=∠DCB,
∴![]() ,
,
∴AD=BD,
∴Rt△ADE≌Rt△BDF(HL),
∴AE=BF,
∴CE+CF=AC﹣AE+CB+BF=AC+BC=m+n,
∴CE=CF=DE=DF=![]() (m+n),
(m+n),
∴CD=![]() (m+n),
(m+n),
故答案为:![]() (m+n).
(m+n).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】已知一次函数y1=kx+m(k≠0)和二次函数y2=ax2+bx+c(a≠0)的自变最x和对应函数值y1,y2的部分对应值如表:
x | … | ﹣1 | 0 | 2 | 4 | … |
y1 | … | 0 | 1 | 3 | 5 | … |
x | … | ﹣1 | 1 | 3 | 4 | … |
y2 | … | 0 | ﹣4 | 0 | 5 | … |
当y1≥y2时,自变量x的取值范图是_____.