题目内容
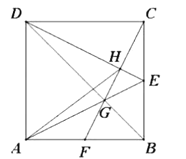
【题目】如图,正方形![]() 的边长为6,点
的边长为6,点![]() 是
是![]() 边的中点,连接
边的中点,连接![]() 与对角线
与对角线![]() 交于点
交于点![]() ,连接
,连接![]() 并延长,交
并延长,交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 。以下结论:①
。以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 。其中正确的结论是( )
。其中正确的结论是( )
A.1B.2C.3D.4
【答案】D
【解析】
根据正方形对角线的性质及全等三角形的性质求证![]() ,从而判断①;延长DE,AB相交于点M,根据条件证出△DCH∽△MFH,从而判断②;根据勾股定理及三角形面积公式求得
,从而判断①;延长DE,AB相交于点M,根据条件证出△DCH∽△MFH,从而判断②;根据勾股定理及三角形面积公式求得![]() ,然后根据△DCG∽△BFG求得
,然后根据△DCG∽△BFG求得![]() ,从而判断④,过点H作HK⊥AB,利用勾股定理和相似三角形的性质求得
,从而判断④,过点H作HK⊥AB,利用勾股定理和相似三角形的性质求得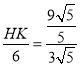 ,
,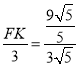 ,求得
,求得![]() ,从而判断③.
,从而判断③.
解:由题意可知:![]()
又∵正方形ABCD中,AB=CB,BG=BG
∴△ABG≌△CBG
∴![]()
又∵点E是BC的中点,
∴CE=BE
又∵正方形ABCD中,AB=CD,![]()
∴△DCE≌△ABE
∴![]()
∵![]()
∴![]() ,即①
,即①![]() 正确;
正确;
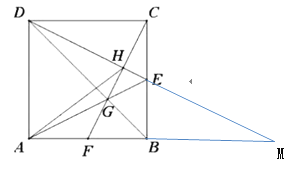
如图:延长DE,AB相交于点M
∵在正方形ABCD中,点E是BC的中点,
∴易证△DCE≌△MBE
∴DC=BM=6
又由①![]() 正确
正确
可得![]()
又∵![]()
∴△DCE≌△CBF
∴BF=CE=3
∵DC∥AB
∴△DCH∽△MFH
∴![]()
∴②![]() 正确;
正确;
由题意可知CE=3,DC=6,∠DCE=90°
∴![]()
又根据三角形面积公式可得:![]()
∴![]()
由△DCE≌△CBF
∴CF=DE
∵DC∥AB
∴△DCG∽△BFG
∴![]() ,即
,即![]()
∴![]()
∴![]() ,④正确.
,④正确.
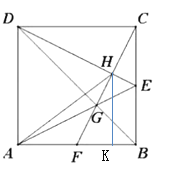
过点H作HK⊥AB
由易证可知![]()
∴![]() ,即
,即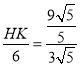
∴![]()
同理:![]() ,即
,即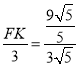
∴![]()
∴![]()
∴在Rt△AHK中,![]()
∴③![]() 正确;正确的共4个,
正确;正确的共4个,
故选:D.

练习册系列答案
相关题目