题目内容
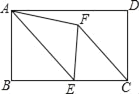
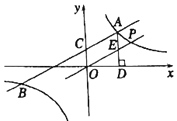
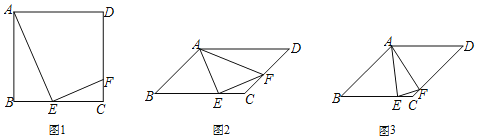
【题目】如图1,在正方形ABCD中,E是边BC的中点,F是CD上一点,已知∠AEF=90°.
(1)求证:![]() ;
;
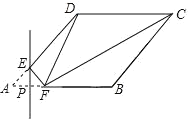
(2)平行四边形ABCD中,E是边BC上一点,F是边CD上一点,∠AFE=∠ADC,∠AEF=90°.
①如图2,若∠AFE=45°,求![]() 的值;
的值;
②如图3,若AB=BC,EC=3CF,直接写出cos∠AFE的值.
【答案】(1)见解析;(2)①![]() ;②cos∠AFE=
;②cos∠AFE=![]()
【解析】
(1)用特殊值法,设![]() ,则
,则![]() ,证
,证![]() ,可求出CF,DF的长,即可求出结论;
,可求出CF,DF的长,即可求出结论;
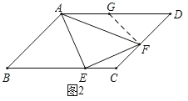
(2)①如图2,过F作![]() 交AD于点G,证
交AD于点G,证![]() 和
和![]() 是等腰直角三角形,证
是等腰直角三角形,证![]() ,求出
,求出![]() 的值,即可写出
的值,即可写出![]() 的值;②如图3,作
的值;②如图3,作![]() 交AD于点T,作
交AD于点T,作![]() 于H,证
于H,证![]() ,设CF=2,则CE=6,可设AT=x,则TF=3x,
,设CF=2,则CE=6,可设AT=x,则TF=3x,![]() ,
,![]() ,分别用含x的代数式表示出∠AFE和∠D的余弦值,列出方程,求出x的值,即可求出结论.
,分别用含x的代数式表示出∠AFE和∠D的余弦值,列出方程,求出x的值,即可求出结论.
(1)设BE=EC=2,则AB=BC=4,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴∠FEC=∠EAB,
又∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
∴CF=1,
则![]() ,
,
∴![]() ;
;
(2)①如图2,过F作![]() 交AD于点G,
交AD于点G,
∵![]() ,
,
∴![]() 和
和![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,![]() ,
,
∴∠AGF=∠C,
又∵![]() ,
,
∴∠GAF=∠CFE,
∴![]() ,
,
∴![]() ,
,
又∵GF=DF,
∴![]() ;
;
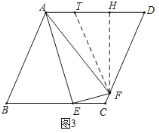
②如图3,作![]() 交AD于点T,作
交AD于点T,作![]() 于H,
于H,
则![]() ,
,
∴![]() ,
,
∴∠ATF=∠C,
又∵![]() ,且∠D=∠AFE,
,且∠D=∠AFE,
∴∠TAF=∠CFE,
∴![]() ,
,
∴![]() ,
,
设CF=2,则CE=6,可设AT=x,则TF=3x,![]() ,
,
∴![]() ,且
,且![]() ,
,
由![]() ,得
,得![]() ,
,
解得x=5,
∴![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目