Question

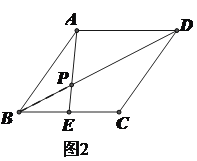
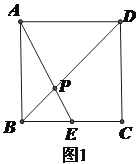
【题目】已知菱形ABCD边长为6，E是BC的中点，AE、BD相交于点P.

（1）如图1，当∠ABC=90°时，求BP的长；

（2）如图2，当∠ABC角度在改变时,BP的中垂线与边BC的交点F的位置是否发生变化?如果不变，请求出BF的长；如果改变，请说明理由；

（3）当∠ABC从90°逐步减少到30°的过程中，求P点经过路线长.

Answer 1

【答案】（1）BP=；（2）点F的位置不发生改变，BF=2；（3）P的路径长为.

【解析】（1）当∠ABC=90°时，菱形ABCD成为正方形;

∵E是BC的中点，BC＝6,

∴BE＝3.由勾股定理得

,

,

,

,

,

.

（2）∵当∠ABC角度在改变时，始终有MF∥AC,

.

∵BN,BO,BC始终不变，

∴点F的位置不发生改变.

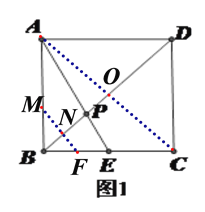
垂直平分 ,

,

.

（3）点P经过的路线是以点P为圆心，以NP为半径，圆心角为60°的一段扇形.

所以路线长为 .