题目内容
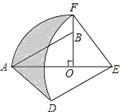
【题目】如图1,已知△ACB和△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,以CE、BC为边作平行四边形CEFB,连CD、CF.
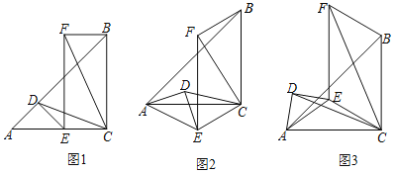
(1)如图2,△ADE绕点A旋转一定角度,求证:CD=![]() CF;
CF;
(2)如图3,AE=![]() ,AB=
,AB=![]() ,将△ADE绕A点旋转一周,当四边形CEFB为菱形时,求CF的长.
,将△ADE绕A点旋转一周,当四边形CEFB为菱形时,求CF的长.
【答案】(1)见解析 (2)6或4
【解析】
(1)连接FD,证明△ADC≌△EDF(SAS),推出△DFC为等腰直角三角形即可解决问题;
(2)分两种情形分别画出图形,利用(1)中结论求出CD即可解决问题.
(1)解:连接FD,设DE与AC交于点G
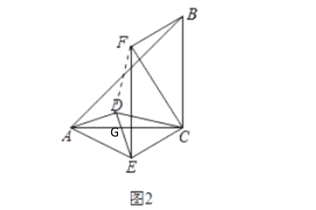
∵四边形CEFB是平行四边形
∴BC∥EF
∵AC⊥BC
∴EF⊥AC
∵AD⊥DE,EF⊥AC,∠DGA=∠CGE
∴∠DAC=∠DEF,
又∵AD=ED,AC=EF,
∴△ADC≌△EDF(SAS),
∴DC=DF,∠ADC=∠EDF,即∠ADE+∠EDC=∠FDC+∠EDC,
∴∠FDC=∠ADE=90°,
∴△DFC为等腰直角三角形,
∴CD=![]() CF;
CF;
(2)解:如图,设AE与CD的交点为M,
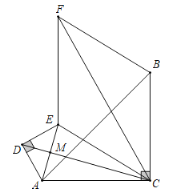
∵四边形CEFB为菱形
∴CE=CB
∵△ADE、△ACB为等腰直角三角形
∴CA=CB
∴CE=CA,
∵DE=DA,
∴CD垂直平分AE,
∵AE=![]() ,AB=
,AB=![]()
∴DM=EM=![]() AE=
AE=![]() ,AC=BC=
,AC=BC=![]() AB=
AB=![]()
∴CE=![]()
∴CM=![]() =
=![]() ,
,
∴CD=DM+CM=![]() ,
,
∵CF=![]() CD,
CD,
∴CF=6;
如图,设AE与CD的交点为M,
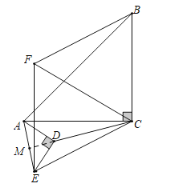
同法可得CD=CM-DM=![]() -
-![]() =
=![]() ,
,
∴CF=![]() CD=4;
CD=4;
综上所述,满足条件的CF的值为6或4.

 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案【题目】某宾馆拥有客房100间,经营中发现:每天入住的客房数y(间)与房价x(元)(180≤x≤300)满足一次函数关系,部分对应值如下表:
x(元) | 180 | 260 | 280 | 300 |
y(间) | 100 | 60 | 50 | 40 |
(1)求y与x之间的函数表达式;
(2)已知每间入住的客房,宾馆每日需支出各种费用100元;每间空置的客房,宾馆每日需支出各种费用60元.当房价为多少元时,宾馆当日利润最大?求出最大利润.(宾馆当日利润=当日房费收入-当日支出)