题目内容
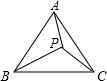 如图,P为等边△ABC内一点,PA、PB、PC的长为正整数,且PA2+PB2=PC2,设PA=m,n为大于5的实数,满m2n+30m+9n≤5m2+6mn+45,求△ABC的面积.
如图,P为等边△ABC内一点,PA、PB、PC的长为正整数,且PA2+PB2=PC2,设PA=m,n为大于5的实数,满m2n+30m+9n≤5m2+6mn+45,求△ABC的面积.
分析:由已知求出PA、PB、PC的长度,设∠PAB=Q,等边三角形的边长是a,∠PAC=60°-Q,根据锐角三角函数(余弦定理)求出cosQ和cos(60°-Q)的值,即可求出a的长度,过A作AD⊥BC于D,求出AD的长度,根据三角形的面积公式即可求出答案.
解答:解:m2n+30m+9n≤5m2+6mn+45,
∴分解因式得:(n-5)(m-3)2≤0,
∵n为大于5的实数,
∴m-3=0,∵即:PA=m=3,
∵PA2+PB2=PC2,PA、PB、PC的长为正整数,
∴PB=4,PC=5,
设∠PAB=Q,等边三角形的边长是a,
则∠PAC=60°-Q,
由余弦定理得:cosQ=
=
,(1)
cos(60°-Q)=
=
,(2)
而cos(60°-Q)=cos60°cosQ-sin60°sinQ,
=
-
=
,(3)
将(1)代入(3)得:
-
=
,
解得:sinQ=
,
∵(sinQ)2+(cosQ)2=1,
∴(
)2+(
)2=1,
令a2=t,
∴
+
=1,
解得:t1=25+12
,t2=25-12
,
由(1)知a>0,cosQ>0,
即
>0,a2>7,
∴t2=25-12
<7,不合题意舍去,
∴t=25-12
,
即a2=25-12
,
过A作AD⊥BC于D,
∵等边△ABC,
∴BD=CD=
a,
由勾股定理得:AD=
a,
∴S△ABC=
•a•
a=
a2=9+
.
答:△ABC的面积是9+
.
∴分解因式得:(n-5)(m-3)2≤0,
∵n为大于5的实数,
∴m-3=0,∵即:PA=m=3,
∵PA2+PB2=PC2,PA、PB、PC的长为正整数,
∴PB=4,PC=5,
设∠PAB=Q,等边三角形的边长是a,
则∠PAC=60°-Q,
由余弦定理得:cosQ=
| AB2+PA2-BP2 |
| 2AB•PA |
| a2-7 |
| 6a |
cos(60°-Q)=
| PA2+AC2-PC2 |
| 2PA•AC |
| a2-16 |
| 6a |
而cos(60°-Q)=cos60°cosQ-sin60°sinQ,
=
| cosQ |
| 2 |
| ||
| 2 |
| a2-16 |
| 6a |
将(1)代入(3)得:
| ||
| 6a |
| ||
| 2 |
| a2-16 |
| 6a |
解得:sinQ=
| 25-a2 | ||
6
|
∵(sinQ)2+(cosQ)2=1,
∴(
| 25-a2 | ||
6
|
| a2-7 |
| 6a |
令a2=t,
∴
| (25-t)2 |
| 108t |
| (t-7)2 |
| 36t |
解得:t1=25+12
| 3 |
| 3 |
由(1)知a>0,cosQ>0,
即
| a2-7 |
| 6a |
∴t2=25-12
| 3 |
∴t=25-12
| 3 |
即a2=25-12
| 3 |
过A作AD⊥BC于D,
∵等边△ABC,
∴BD=CD=
| 1 |
| 2 |
由勾股定理得:AD=
| ||
| 2 |
∴S△ABC=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
| 25 |
| 4 |
| 3 |
答:△ABC的面积是9+
| 25 |
| 4 |
| 3 |
点评:本题主要考查了勾股定理的逆定理,用公式法解一元二次方程,用提取公因式法分解因式,余弦定理等知识点,运用余弦定理求等边三角形的边长是解此题的关键.题型较好但难度较大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 3、如图,△ABC为等边三角形,∠ABC、∠ACB的平分线相交于点O,OE∥AB交BC于点E,OF∥AC交BC于点F,图中等腰三角形共有( )
3、如图,△ABC为等边三角形,∠ABC、∠ACB的平分线相交于点O,OE∥AB交BC于点E,OF∥AC交BC于点F,图中等腰三角形共有( ) 如图,△ABC为等边三角形,点D,E,F分别在AB,BC,CA边上,且△DEF是等边三角形,求证:△ADF≌△CFE.
如图,△ABC为等边三角形,点D,E,F分别在AB,BC,CA边上,且△DEF是等边三角形,求证:△ADF≌△CFE. 如图,△ABC为等边三角形,AD为BC边上的高,且AB=2,则正方形ADEF的面积为
如图,△ABC为等边三角形,AD为BC边上的高,且AB=2,则正方形ADEF的面积为 (2013•普陀区模拟)如图,△AOB为等边三角形,点B的坐标为(-2,0),过点C(2,0)作直线l交AO于点D,交AB于E,点E在反比例函数
(2013•普陀区模拟)如图,△AOB为等边三角形,点B的坐标为(-2,0),过点C(2,0)作直线l交AO于点D,交AB于E,点E在反比例函数 如图,△AOB为等边三角形,点B的坐标为(-2,0),过点C(2,0)作直线l交AO于D,交AB于E,点E在某反比例函数图象上,当△ADE和△DCO的面积相等时,那么该反比例函数解析式为( )
如图,△AOB为等边三角形,点B的坐标为(-2,0),过点C(2,0)作直线l交AO于D,交AB于E,点E在某反比例函数图象上,当△ADE和△DCO的面积相等时,那么该反比例函数解析式为( )