题目内容
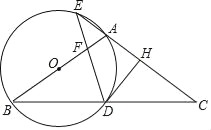
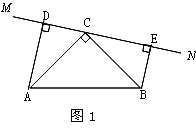
【题目】如图,在△ABC中,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,且
,且![]() 于
于![]() ,
,![]() 于
于![]() .
.
(1)当直线![]() 绕点
绕点![]() 旋转到图1的位置时,
旋转到图1的位置时,
①求证:△ADC≌△CEB.
②求证:DE=AD+BE.
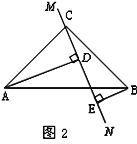
(2)当直线![]() 绕点
绕点![]() 旋转到图2的位置时,判断
旋转到图2的位置时,判断![]() 和
和![]() 的关系,并说明理由.
的关系,并说明理由.
【答案】(1)①见解析;②见解析;(2)△ADC≌△CEB;理由见解析
【解析】
(1)①要证△ADC≌△CEB,已知一直角∠ADC=∠CEB=90°和一边AC=CB对应相等,由题意根据同角的余角相等,可得另一内角∠ECB=∠DAC,再由AAS即可判定;
②由①得出AD=CE,BE=CD,而DE=CD+CE,故DE=AD+BE;
(2)同理,根据上一小题的解题思路,易得△ADC≌△CEB.
(1)①∵∠ACB=90°
∴∠DCA+∠ECB=90°
又∵AD⊥MN
∴∠DCA+∠DAC=90°
∴∠ECB=∠DAC
又∵AD⊥MN,BE⊥MN
∴∠ADC=∠CEB=90°
在△ADC和△CEB中
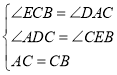
∴△ADC≌△CEB(AAS)
②∵△ADC≌△CEB
∴AD=CE,BE=CD
又∵DE=CD+CE
∴DE=AD+BE
(2)△ADC≌△CEB;
∵∠ACB=90°
∴∠DCA+∠ECB=90°
又∵AD⊥MN
∴∠DCA+∠DAC=90°
∴∠ECB=∠DAC
又∵AD⊥MN,BE⊥MN
∴∠ADC=∠CEB=90°
在△ADC和△CEB中
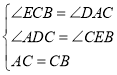
∴△ADC≌△CEB(AAS)

【题目】某股民上星期五买进某公司股票1000股,每股27元,下表为本周内每日该股票的涨跌情况(单位:元)(周六、周日休盘)
星期 | 一 | 二 | 三 | 四 | 五 |
每股 涨跌 | +4 | +4.5 | -1 | -1.5 | -4 |
(1)星期五收盘时,每股是多少元?
(2)本周内最高价是每股多少元?最低价是每股多少元?
(3)已知该股民买进股票时付了0.15%的手续费,卖出时需付成交额0.15%的手续费和0.1%的交易税,若该股民在星期五收盘前将全部股票卖出,他的收益情况如何?