题目内容
【题目】已知△ABC是等边三角形,点D在BC边上,点E在AB的延长线上,将DE绕D点顺时针旋转120°得到DF.

(1)如图1,若点F恰好落在AC边上,求证:点D是BC的中点;
(2)如图2,在(1)的条件下,若![]() =45°,连接AD,求证:
=45°,连接AD,求证:![]() ;
;
(3)如图3,若![]() ,连CF,当CF取最小值时,直接写出
,连CF,当CF取最小值时,直接写出![]() 的值.
的值.
【答案】(1)详见解析;(2)详见解析;(3)3.
【解析】
(1)要证明D是线段的中点,最常见的作法是证明两线段所在三角形全等,过点D作DH⊥AB,DG⊥AC,构建出线段所在的三角形,然后根据四边形内角和,确定相等的角,根据旋转的性质确定相等的边,求![]() ,根据三角形全等的性质,得到条件进而求证
,根据三角形全等的性质,得到条件进而求证![]() 解决.
解决.
(2)设出CG为x,根据等边三角形的性质和直角三角形中锐角三角函数,将BE、CF、AD的边分别用x表示出来,进而求证![]() 即可.
即可.
(3)延长DB至点K,使BK=BE,过点D作DQ∥AB且DQ=AB,连接AQ,根据平行线的性质和等边三角形的性质,证明△DEK≌DFQ,得出∠FQD=60°,FQ所在直线即为F的轨迹,然后根据直角三角形中边角关系,判断出CD与PD的关系,然后确定PD与CQ的关系,最后确定![]() 的值即可.
的值即可.
解:(1) 过点D作DH⊥AB,DG⊥AC,如图:
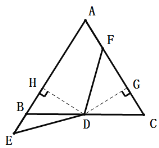
∵△ABC是等边三角形
∴∠ A=∠ C=∠ ABC=60°
∵∠EDF=120°,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
故D为BC的中点
(2)证明:
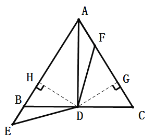
∵△ABC为等边三角形,
∴∠A=∠B=∠C=60°
设CG为m,
在Rt△CGD中,![]()
![]()
在Rt△FGD中,
∵∠DFG=45°
∴DG=GF=![]()
![]()
∴CF=CG+GF=![]()
∵D是BC的中点
∴BD=CD=2m
在Rt△BDH中,
BH=BD×cos60°=2m×![]() =m
=m
![]()
∵DF是由DE旋转得到
∴DE=DF=![]()
在Rt△EDH中,
![]()
BE=EH-BH=![]() -m=
-m=![]()
∴CF+BE=![]() +
+![]()
在Rt△ADC中,
AD=CD×tan60°=2m×![]() =
=![]()
∴CF+BE=AD
(3)解:

延长DB至点K,使BK=BE
过点D作DQ∥AB且DQ=AB,连接AQ
∵BE=CD,BE=BK
∴BK=CD
∴BC=BD+CD=BD+BK=DK
∵△ABC是等边三角形
∴AB=BC=AC
∵DQ=AB,
∴DK=DQ
∵DQ∥AB
∠BDQ+∠ABC=120°
∵∠BDF=120°
∴∠EDB=∠FDQ
在△DEK和DFQ中
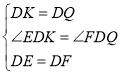
∴△DEK≌DFQ(SAS)
∴∠FQD=∠K
∵△ABC为等边三角形
∴∠ABC=60°
又∵BK=NE,∠KBE=∠ABC=60°
∴∠K=∠BEK=60°
∠FQD=∠K=60°
∴F的轨迹为直线FQ,
∴当CF⊥FQ时,CF最小,此时DQ与CF相交于点P,
在Rt△PFQ中,
∵∠FPQ=90°-60°
∴PQ=2FQ
∵∠BDQ=120°,
∴∠PDC=60°,
在△FQP和△CDP中,
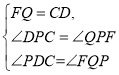
∴△FQP≌△CDP(AAS)
∴PQ=PD
在Rt△PDC中,
∵∠PDC=∠PQF=60°
∴![]()
PQ=2CD
∴DQ=4CD
∴KD=4CD
又∵KB=CD
∴![]()

【题目】某商场经营某种品牌的玩具,进价是![]() 元,根据市场调查:在一段时间内,销售单价是
元,根据市场调查:在一段时间内,销售单价是![]() 元时,销售量是
元时,销售量是![]() 件,而销售单价每涨
件,而销售单价每涨![]() 元,就会少售出
元,就会少售出![]() 件玩具.
件玩具.
![]() 不妨设该种品牌玩具的销售单价为
不妨设该种品牌玩具的销售单价为![]() 元
元![]() ,请你分别用
,请你分别用![]() 的代数式来表示销售量
的代数式来表示销售量![]() 件和销售该品牌玩具获得利润
件和销售该品牌玩具获得利润![]() 元,并把结果填写在表格中:
元,并把结果填写在表格中:
销售单价(元) |
|
销售量 | ________ |
销售玩具获得利润 | ________ |
![]() 在
在![]() 问条件下,若商场获得了
问条件下,若商场获得了![]() 元销售利润,求该玩具销售单价
元销售利润,求该玩具销售单价![]() 应定为多少元.
应定为多少元.
![]() 在
在![]() 问条件下,若玩具厂规定该品牌玩具销售单价不低于
问条件下,若玩具厂规定该品牌玩具销售单价不低于![]() 元,且商场要完成不少于
元,且商场要完成不少于![]() 件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?





