题目内容
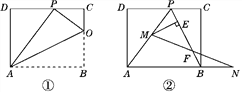
【题目】如图,点D,E,F分别在等边三角形ABC的三边上,且DE⊥AB,EF⊥BC,FD⊥AC,过点F作FH⊥AB于H,则![]() 的值为_________.
的值为_________.

【答案】![]()
【解析】
设AH为x,利用等边三角形的性质和直角三角形中边角关系,求证三角形DEF也为等边三角形,将BC用x表示出来,然后求解即可.
∵△ABC是等边三角形,
∴AB=AC=BC,
∠A=∠B=∠C=60°.
∵DE⊥AB,EF⊥BC,FD⊥AC,
∴∠AFD=∠BDE=∠FEC=90°
∠ADF=∠BED=∠CFE=90°-60°=30°
∴∠DEF=∠DFE=∠EDF=180°-30°-90°=60°
故△DEF是等边三角形
∴DE=DF=EF
又∵∠A=∠B=∠C, ∠AFD=∠BDE=∠FEC
∴△ADF≌△BED≌△CEF
∴AD=BE,AF=CF
设AH为x,则AF=2x
在Rt△ADF中,∠ADF=30°,
∴AD=4x
∴BE=4x,CF=2x
BC=2x+4x=6x
∴![]() =
=![]()
故答案为:![]()

练习册系列答案
相关题目