题目内容
【题目】如图,某中学准备在校园里利用院墙的一段再围三面篱笆,形成一个矩形花园![]() (院墙
(院墙![]() 长
长![]() 米),现有
米),现有![]() 米长的篱笆.
米长的篱笆.

(1)请你设计一种围法(篱笆必须用完),使矩形花园的面积为![]() 米.
米.
(2)如何设计可以使得围成的矩形面积最大?最大面积是多少?
【答案】见详解.
【解析】
(1)设AB为xm,则BC为(40-2x)m,根据题意可得等量关系:矩形的面积=长×宽=150,根据等量关系列出方程,再解即可;
(2)根据题意和图形可以得到S与x之间的函数关系,将函数关系式化为顶点式,即可解答本题.
解:(1)设AB为xm,则BC为(40-2x)m,根据题意可得:
X(40-2x)=150
解得:x1=![]() ,x2=15.
,x2=15.
:当x=![]() 时,40-2x=30>25.故不满足题意,应舍去.
时,40-2x=30>25.故不满足题意,应舍去.
②当x=15时,40-2x=10<25,故当x=15时,满足实际要求.
∴当x=15 时,使矩形花园的面积为![]() 米.
米.
(2)设矩形的面积为S,则依意得:
S= X(40-2x)=-2x2+40x=-2(x-5)2+50
∴当x=5,时S有最大值.最大值为50.

 黄冈创优卷系列答案
黄冈创优卷系列答案【题目】为鼓励居民节约用电,某市采用价格调控手段达到省电目的,该市电费收费标准如下表(按月结算):
每月用电量度 | 电价/(元/度) |
不超过150度的部分 | 0.50元/度 |
超过150度且不超过250度的部分 | 0.65元/度 |
超过250度的部分 | 0.80元/度 |
问:(1)某居民12月份用电量为180度,请问该居民12月应缴交电费多少元?
(2)设某月的用电量为![]() 度(
度(![]() ),试写出不同电量区间应缴交的电费.
),试写出不同电量区间应缴交的电费.
【题目】为了加强公民的节水意识,合理利用水资源,某区采用价格调控手段达到节水的目的,如表是调控后的价目表.
价目表
每月用水量 | 单价 |
不超过6吨的部分 | 2元/吨 |
超出6吨不超出10吨的部分 | 4元/吨 |
超出10吨的部分 | 8元/吨 |
注:水费按月结算.
(1)若该户居民8月份用水8吨,则该用户8月应交水费 元;若该户居民9月份应交水费26元,则该用户9月份用水量为 吨;
(2)若该户居民10月份应交水费30元,求该用户10月份用水量;
(3)若该户居民11月、12月共用水18吨,共交水费52元,求11月、12月各应交水费多少元?
【题目】某制笔企业欲将200件产品运往![]() ,
,![]() ,
,![]() 三地销售,要求运往
三地销售,要求运往![]() 地的件数是运往
地的件数是运往![]() 地件数的2倍,各地的运费如图所示.设安排
地件数的2倍,各地的运费如图所示.设安排![]() 件产品运往
件产品运往![]() 地.
地.
|
|
| |
产品件数(件) |
|
| |
运费(元) |
|
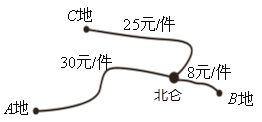
(1)①根据信息补全上表空格.②若设总运费为![]() 元,写出
元,写出![]() 关于
关于![]() 的函数关系式及自变量的取值范围.
的函数关系式及自变量的取值范围.
(2)若运往![]() 地的产品数量不超过运往
地的产品数量不超过运往![]() 地的数量,应怎样安排
地的数量,应怎样安排![]() ,
,![]() ,
,![]() 三地的运送数量才能达到运费最少.
三地的运送数量才能达到运费最少.