题目内容
已知:点P(a+1,a-1)关于x轴的对称点在反比例函数y=-
(x>0)的图象上,y关于x的函数y=k2x2-(2k+1)x+1的图象与坐标轴只有两个不同的交点A﹑B,求P点坐标和△PAB的面积.
| 8 |
| x |
(1)∵P点关于x轴的对称点为(a+1,-a+1),它在y=-
(x>0)图象上,且在第四象限
∴(a+1)(-a+1)=-8,即a2=9
∴a=3(a=-3舍去)
∴P(4,2)(2分)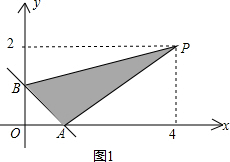
(2)当k=0时,y=-x+1,
设一次函数图象与x轴交于A,与y轴交于B,则A(1,0),B(0,1)
此时,S△PAB=
×(1+2)×4-
×1×1-
×3×2=
(4分)
当k≠0时,函数y=k2x2-(2k+1)x+1的图象为抛物线,与y轴交于B(0,1)
∵它的图象与坐标轴只有两个交点
∴它的图象与x轴只有一个交点,设为A点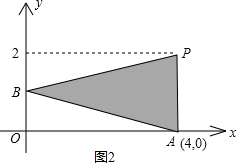
∴△=(2k+1)2-4k2=0
解得:k=-
(5分)
∴抛物线y=
x2-
x+1=
(x-4)2与x轴交于A(4,0)
∴此时,S△PAB=
×2×4=4
综合得:△PAB的面积为
或4.(7分)
| 8 |
| x |
∴(a+1)(-a+1)=-8,即a2=9
∴a=3(a=-3舍去)
∴P(4,2)(2分)

(2)当k=0时,y=-x+1,
设一次函数图象与x轴交于A,与y轴交于B,则A(1,0),B(0,1)
此时,S△PAB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
当k≠0时,函数y=k2x2-(2k+1)x+1的图象为抛物线,与y轴交于B(0,1)
∵它的图象与坐标轴只有两个交点
∴它的图象与x轴只有一个交点,设为A点

∴△=(2k+1)2-4k2=0
解得:k=-
| 1 |
| 4 |
∴抛物线y=
| 1 |
| 16 |
| 1 |
| 2 |
| 1 |
| 16 |
∴此时,S△PAB=
| 1 |
| 2 |
综合得:△PAB的面积为
| 5 |
| 2 |

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
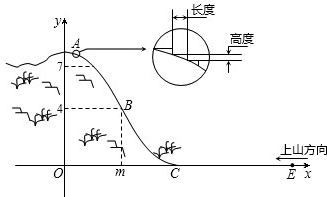 试求索道的最大悬空高度.
试求索道的最大悬空高度.
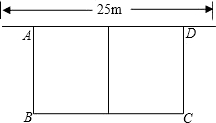
 ______m2、______m2,在这些数中,x取______m时,面积S最大.
______m2、______m2,在这些数中,x取______m时,面积S最大.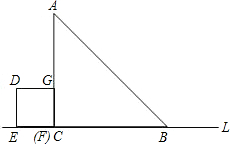 1cm的速度作匀速运动,最后点E与点B重合.
1cm的速度作匀速运动,最后点E与点B重合. 不存在,请说明理由.
不存在,请说明理由.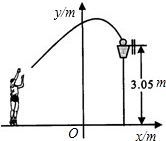 单位:m).请你根据所得的解析式,回答下列问题:
单位:m).请你根据所得的解析式,回答下列问题: