题目内容
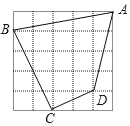
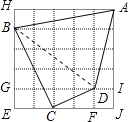
【题目】如图，在5×5的方格纸中，每一个小正方形的边长都为1．
（1）∠BCD是不是直角？请说明理由；
（2）求四边形ABCD的面积．
【答案】（1）见解析；（2）
【解析】试题分析：（1）连接BD，由于每一个小正方形的边长都为1，根据勾股定理可分别求出△BCD的三边长，根据勾股定理的逆定理即可判断出△BCD的形状；
（2）S四边形ABCD=S正方形AHEJ-S△BCE-S△ABH-S△ADI-S△DCF-S正方形DFJI．
试题解析：（1）∠BCD是直角，理由如下：连接BD，
∵BC=
=2
，CD=
=
，BD=
=5，
∴BC2+CD2=BD2，
∴∠BCD为直角；
（2）S四边形ABCD=S正方形AHEJ-S△BCE-S△ABH-S△ADI-S△DCF-S正方形DFJI，
所以S四边形ABCD=5×5﹣
×4×2﹣
×2×1﹣1×1﹣
×4×1﹣
×5×1，
=25﹣4﹣1﹣1﹣2﹣
=
．
练习册系列答案
阅读快车系列答案
相关题目
【题目】小颖和小红两位同学在学习“概率”时，做投掷骰子（质地均匀的正方体）试验，她们共做了60次试验，试验的结果如下：
朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现的次数 | 7 | 9 | 6 | 8 | 20 | 10 |
（1）计算“3点朝上”的频率和“5点朝上”的频率.
（2）小颖说：“根据上述试验，一次试验中出现5点朝上的概率最大”；小红说：“如果投掷600次，那么出现6点朝上的次数正好是100次”.小颖和小红的说法正确吗？为什么？
