题目内容
【题目】已知等腰Rt△ABC中,∠BAC=90°.点D从点B出发沿射线BC移动,以AD为腰作等腰Rt△ADE,∠DAE=90°.连接CE.

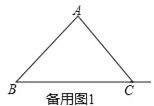

(1)如图,求证:△ACE≌△ABD;
(2)点D运动时,∠BCE的度数是否发生变化?若不变化,求它的度数;若变化,说明理由;
(3)若AC=![]() ,当CD=1时,请求出DE的长.
,当CD=1时,请求出DE的长.
【答案】(1)见解析;(2)90°;(3)DE的长为![]() 或
或![]() .
.
【解析】试题分析:(1)由△ABC和△ADE都是等腰Rt△可得,AB=AC,AD=AE,∠BAC=∠DAE=90°,则有∠BAD=∠CAE,从而可证到△ACE≌△ABD;
(2)由△ACE≌△ABD可得∠ACE=∠ABD=45°,从而得到∠BCE=∠BCA+∠ACE=90°;
(3)可分点D在线段BC上时(如图1)和点D在线段BC延长线上时(如图2)两种情况讨论,在Rt△ABC中运用勾股定理可求出BC,从而得到BD,由△ACE≌△ABD可得CE=BD,在Rt△DCE中运用勾股定理就可求出DE.
试题解析:(1)∵△ABC和△ADE都是等腰Rt△,
∴AB=AC,AD=AE,∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
在△ACE和△ABD中,
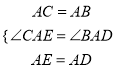 ,
,
∴△ACE≌△ABD;
(2)∵△ACE≌△ABD,
∴∠ACE=∠ABD=45°,
∴∠BCE=∠BCA+∠ACE=45°+45°=90°;
∴∠BCE的度数不变,为90°;
(3)①点D在线段BC上时,如图1,
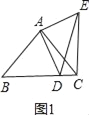
∵AB=AC=![]() ,∠BAC=90°,
,∠BAC=90°,
∴BC=![]() ,
,
∵CD=1,
∴BD=![]() ﹣1,
﹣1,
∵△ACE≌△ABD,
∴CE=BD=![]() ﹣1.
﹣1.
∵∠BCE=90°,
∴DE=![]() ;
;
②点D在线段BC延长线上时,如图2,
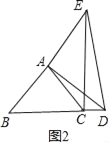
∵AB=AC=![]() ,∠BAC=90°,
,∠BAC=90°,
∴BC=![]() ,
,
∵CD=1,
∴BD=![]() +1,
+1,
∵△ACE≌△ABD,
∴CE=BD=![]() +1,
+1,
∵∠BCE=90°,
∴∠ECD=90°,
∴DE=![]() ,
,
综上所述:DE的长为![]() 或
或![]() .
.

 一课一练课时达标系列答案
一课一练课时达标系列答案